Аналитические методы решения уравнения теплопроводности

АНАЛИТИЧЕСКИЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ

В настоящее время аналитическим путем решено очень большое количество одномерных задач теплопроводности.

А.В.Лыков, например, рассматривает четыре метода решения уравнения теплопроводности в условиях одномерной задачи: метод разделения переменных, метод источников, операционный метод, метод конечных интегральных преобразований.

В дальнейшем остановимся только на первом методе, получившем наибольшее распространение.

Метод разделения переменных при решении уравнения теплопроводности Дифференциальное уравнение теплопроводности в условиях одномерной задачи и без источников теплоты имеет вид.

?t/?ф = a ?²t/?x².(3.1).

Это уравнение является частным случаем однородного дифференциального уравнения с постоянными коэффициентами для некоторой функции t от двух переменных x и ф:

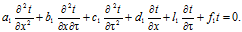
(3.2).

Легко проверить, что частным решением этого уравнения будет выражение.

t = C exp (бx + вф).(3.3).

Действительно:

• ?t/?x = бС ехр (бx + вф);?t/?ф = вС ехр (бx + вф);
• ?²t/?x² = б²С ехр (бx + вф);
• ?²t/?ф² = в²С ехр (бx + вф);?²t/(?x ?ф) = бвС ехр (бx + вф).(3.4)

Совместное решение последних семи уравнении дает.

a₁б² + b₁бв + c₁в² + d₁б + l₁в + f₁ = 0.(3.5).

Последнее уравнение называется уравнением коэффициентов.

Переходя к уравнению (3.1) сопоставляя его с уравнением (3.2), заключаем, что.

b₁ = c₁ = d₁ = f₁ = 0;a₁= - a;l₁ = 1.(3.6).

Уравнение коэффициентов (3.5) для частного случая уравнения (3.1) приобретает вид.

— б²a + в = 0(3.7).

или в = б²a.(3.8).

Таким образом, частное решение (3.3) является интегралом дифференциального уравнения (3.1) и с учетом (3.8) приобретет вид.

t = C exp (б²aф + бx).(3.9).

В этом уравнении можно задавать любые значения чисел для C, б, a.

Выражение (3.9) может быть представлено в виде произведения.

t = C exp (б²aф) exp (бx),(3.10).

где сомножитель exp (б²aф) является функцией только времени ф, а сомножитель exp (бx) — только расстояния x:

exp (б²aф) = f (ф);exp (бx) = ц (x).(3.11).

С увеличением времени ф температура во всех точках непрерывно растет и может стать выше наперед заданной, что в практических задачах не встречается. Поэтому обычно берут только такие значения б, при которых б² отрицательно, что возможно при б чисто мнимой величине. Примем б = ± iq,(3.12).

где q — произвольное действительное число (ранее значком q обозначали удельный тепловой поток),.

В этом случае уравнение (3.10) приобретет следующий вид:

t = C exp (- q²aф) exp (± iqx).(3.13).

Обращаясь к известной формуле Эйлера.

exp (± ix) = cos x ± i sin x (3.14).

и, пользуясь ею, преобразуем уравнение (3.13). Получим два решения в комплексном виде:

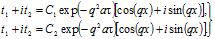
(3.15).

Суммируем левые и правые части уравнений (3.15), затем отделим действительные от мнимых частей в левой и правой частях суммы и приравняем их соответственно. Тогда получим два решения:

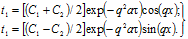
(3.16).

Введем обозначения:

(C₁ + C₂)/2 = D;(C₁ — C₂)/2 = C (3.17).

тогда получим два решения, удовлетворяющих дифференциальному уравнению теплопроводности (3.1):

t₁ = D exp (- q²aф) cos (qx);t₂ = C exp (- q²aф) sin (qx).(3.18).

Известно, что если искомая функция имеет два частных решения, то и сумма этих частных решений будет удовлетворять исходному дифференциальному уравнению (3.1), т. е. решением этого уравнения будет.

t = C exp (- q²aф) sin (qx) + D exp (- q²aф) cos (qx),(3.19).

а общее решение, удовлетворяющее этому уравнению, можно записать в следующем виде:

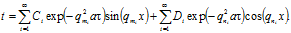
(3.20).

Любые значения q_m, q_n, C_i, D_i в уравнении (3.20) будут удовлетворять уравнению (3.1). Конкретизация в выборе этих значений будет определяться начальными и граничными условиями каждой частной практической задачи, причем значения q_m и q_n определяются из граничных условий, а C_i, и D_i, — из начальных.

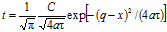
Помимо общего решения уравнения теплопроводности (3.20) в котором имеет место произведение двух функций, одна из которых зависит от x, а другая — от ф, существуют еще решения, в которых такое разделение невозможно, например:

(3.21).

(3.22).

Оба решения удовлетворяют уравнению теплопроводности, в чем легко убедиться, продифференцировав их сначала по ф, а затем 2 раза по x и подставив результат в дифференциальное уравнение (3.1).

Частный пример нестационарного температурного поля в стенке Рассмотрим пример применения полученного выше решения.

Исходные данные.

• 1. Дана бетонная стенка толщиной 2X = 0,80 м.
• 2. Температура окружающей стенку среды и = 0 °C.
• 3. В начальный момент времени температура стенки во всех точках F (x)=1°C.
• 4. Коэффициент теплоотдачи стенки б=12,6Вт/(м²· °С); коэффициент теплопроводности стенки л=0,7Вт/(м· °С); плотность материала стенки с=2000кг/м³; удельная теплоемкость c=1,13· 10³Дж/(кг·°С); коэффициент температуропроводности a=1,1· 10^-3м²/ч; относительный коэффициент теплоотдачи б/л = h=18,0 1/м. Требуется определить распределение температуры в стенке через 5 ч после начального момента времени.

Решение. Обращаясь к общему решению (3.20) и имея в виду, что начальное и последующие распределения температуры симметричны относительно оси стенки, заключаем, что ряд синусов в этом общем решении отпадает, и при x = Х оно будет иметь вид.

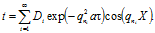
(3.23).

Значения определены из граничных условий (без дополнительных здесь пояснений) и приведены в табл.3.1.

Располагая значениями из табл.3.1, находим искомый ряд значений по формуле.

(3.24).

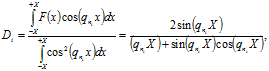
Таблица 3.1 Значения функций, входящих в формулу (3.24)

т. е. Д1 = 1,250; Д2 = — 0,373; Д3 = 0,188; Д4 = — 0,109; Д5 = 0,072.

Начальное распределение температуры в рассматриваемой стенке приобретет следующий вид:

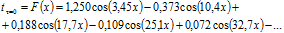
(3.25).

Чтобы получить расчетное распределение температуры через 5 ч после начального момента, необходимо определить ряд значений на время через 5 ч. Эти расчеты выполнены в табл.3.2.

Таблица 3.2 Значения функций, входящих в формулу (3.23)

Окончательное выражение для распределения температуры в толще стенки через 5 ч после начального момента.

(3.26).

На рис. 3.1 показано распределение температуры в толще стенки на начальный момент времени и через 5 ч. Наряду с общим решением здесь же изображены и частные, причем римскими цифрами указаны частные кривые, отвечающие последовательным слагаемым рядов (3.25) и (3.26).

Рис. 3.1. Распределение температуры в стенке на начальный момент времени (слева) и через 5 ч (справа) [8]

При решении практических задач обычно нет необходимости определять температуру во всех точках стенки. Можно ограничиться расчетом температуры лишь для какой-либо одной точки, например для точки в середине стенки. В этом случае объем вычислительных работ по формуле (3.23) значительно сократится.

Если начальная температура в рассмотренном выше случае равна не 1 °C, а Т_с, то уравнение (3.20) примет вид.

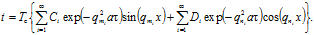
(3.27).

Решение уравнения теплопроводности при различных граничных условиях [8].

Не будем приводить последовательный ход решения уравнения теплопроводности при других граничных условиях, которые имеют практическое значение в решении некоторых задач. Ниже ограничимся лишь формулировкой их условий с показом имеющихся готовых решений.

Исходные данные. Стенка имеет толщину 2Х. В начальный момент во всех ее точках, кроме поверхности, температура Т_с Температура на поверхности 0 °C удерживается в течение всего расчетного периода.

Требуется найти t = f (x, ф).

Решение.

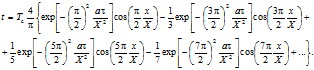
(3.28).

Неподвижное водохранилище покрылось льдом при температуре наибольшей плотности воды (Т_с = 4°С). Глубина водохранилища 5 м (Х = 5 м). Рассчитать температуру воды в водохранилище через 3 месяца после ледостава. Температуропроводность неподвижной воды a = 4,8· 10^-4 м²/ч. Тепловой поток у дна, т. е. при x = 0, отсутствует.

В течение расчетного периода (ф=3· 30·24=2160ч) температура на поверхности удерживается постоянной и равной нулю, т. е. при x = Х Т_п = 0 °C. Весь расчет сводим в табл. 3 и 4. Эти таблицы позволяют вычислить значения температуры через 3 месяца после начального момента для глубин у дна, а затем выше через 1 м, т. е. t_0(дно) = 4 °C; t₁ = 4 °C; t₂ = 3,85°С; t₃ = 3,30°С; t₄ = 2,96°С; t_5(пов) = 0 °C.

Таблица 3.3.

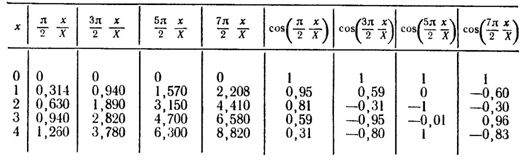
Таблица 3.4.

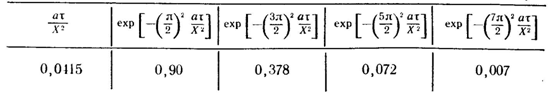
Как видим, в абсолютно неподвижной воде температурные возмущения весьма медленно проникают вглубь. В природных условиях в водоемах под ледяным покровом всегда наблюдаются течения либо гравитационные (проточные), либо конвективные (разноплотностные), либо, наконец, вызванные поступлением грунтовых вод. Все многообразие указанных природных особенностей следует учитывать при практических расчетах, а рекомендации к этим расчетам можно найти в пособиях и в работах К. И. Россинского [37].

Тело ограничено с одной стороны (полуплоскость). В момент времени ф = 0 во всех точках температура тела равна Т_с. Для всех моментов времени ф > 0 на поверхности тела поддерживается температура Т_п = 0 °C.

Требуется найти распределение температуры в толще тела и потерю теплоты через свободную поверхность как функцию времени: t = f (x, ф),.

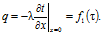
Решение. Температура в любой точке тела и в любой момент времени.

(3.29).

где есть интеграл Гаусса. Его значения в зависимости от функции даны в табл.3.5.

Таблица 3.5.

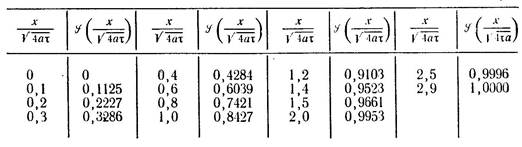
Практически решение начинается с определения отношения, в котором х и ф заданы в условии задачи.

Количество теплоты, теряемой единицей поверхности тела в окружающую среду, определяется по закону Фурье. За весь расчетный период с начального момента до расчетного.

(3.30).

В начальный момент времени температура почвы от поверхности до значительной глубины была постоянной и равной 6 °C. В этот момент температура на поверхности почвы упала до 0 °C.

Требуется определить температуру почвы на глубине 0,5 м через 48 ч при значении коэффициента температуропроводности почвы a = 0,001 м²/ч, а также оценить количество теплоты, теряемое поверхностью за это время.

По формуле (3.29) температура почвы на глубине 0,5 м через 48 ч t=6· 0,87=5,2°С.

Общее же количество теплоты, потерянной единицей поверхности почвы, при коэффициенте теплопроводности л = 0,35 Вт/(м· °С), удельной теплоемкости c = 0,83· 10³ Дж/(кг· °С) и плотности с = 1500 кг/м³ определим по формуле (3.30) Q=l, 86· 10⁶ Дж/м².

интегральный теплопроводность теплота тело.

Рис. 3.2 Распределение температуры по глубине толщи [8]

Вследствие некоторого внешнего воздействия температура поверхности тела, ограниченного с одной стороны (полуплоскость), претерпевает периодические колебания около нуля. Будем считать, что эти колебания гармонические, т. е. температура поверхности меняется по косинусоиде:

(3.31).

где — продолжительность колебания (период), T₀ — температура поверхности,.

T_{0 макс} — ее максимальное отклонение,.

Требуется определить температурное поле как функцию времени.

Решение.

(3.32).

Амплитуда колебаний температуры меняется с x по следующему закону (рис. 3.2):

(3.33).

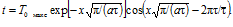
Пример к задаче № 3. Изменение температуры на поверхности сухой песчаной почвы в течение года характеризуется косинусоидальным ходом. Средняя годовая температура при этом равна 6 °C при максимальных отклонениях от средней летом и зимой, достигающих 24 °C.

Требуется определить температуру грунта на глубине 1 м в момент, когда температура на поверхности равна 30 °C (условно 1/VII).

Выражение косинусоиды (3.31) применительно к данному случаю (температуре поверхности) при T_{0 макс} = 24⁰С примет вид Т₀ = 24 cos (2рф/8760) + 6.

Ввиду того, что поверхность грунта имеет среднюю годовую температуру 6 °C, а не нуль, как в уравнении (3.32), расчетное уравнение примет следующий вид:

(3.34).

Приняв для грунта коэффициент температуропроводности a = 0,001 м²/ч и имея в виду, что по условию задачи необходимо определить температуру на конец расчетного периода (через 8760 ч от начального момента), найдем.

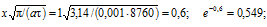
Расчетное выражение (3.34) приобретет следующий вид: t = 24e^-0,6· 0,825 + 6 = 16,9 °С.

На той же глубине 1 м максимальная амплитуда годового колебания температуры, согласно выражению (3.33), составит.

T_{1 макс} = 24e^-0,6 = 13,2 °С, а максимальная температура на глубине 1 м.

t_{1 макс} = T_x макс + 6 = 13,2 + 6 =19, 2 °C.

В заключение отметим, что рассмотренные задачи и подходы могут быть использованы при решении вопросов, связанных с выпуском теплой воды в водоем, а также при химическом методе определения расхода воды и в других случаях.