Проверка гипотез с помощью распределения хи-квадрат

Распределение хи-квадрат (х²) также известно под названием «распределение Пирсона». По аналогии с применением распределения Стьюдента в проверке статистических гипотез рассмотрим вначале, как связаны нормальное распределение с распределением х²* Если случайная величина 2 имеет стандартное нормальное распределение, т. е.

где t = 0,1,…, Г, причем все z_t независимы друг от друга, то величина, рассчитанная по формуле.

будет распределена по у} с Г степенями свободы¹:

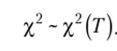
Как видим, в основе распределения х² лежит сумма квадратов нормального распределения. Типичная гипотеза, проверяемая с помощью х²> — это гипотеза о дисперсии.

Пример Некая фирма разработала математическую модель для оценки продаж продукции по дням. Считается, что если стандартное отклонение фактических значений от расчетных за прошедший месяц не превысило 50 единиц, то продажи продукции не претерпевают значительных изменений, модель дает все такой же точный прогноз. Если же стандартное отклонение превышает это значение, то модель требует переоценки. За прошедший месяц (в котором был 31 день) стандартное отклонение составило 55 единиц. Стоит ли пересчитывать коэффициенты модели?

Вешпцель Е. С. Теория вероятностей: учебник. 11-е изд. С. 171.

Сформулируем нулевую и альтернативную гипотезы: Я₀: ст² = 2500, Я: а² >2500.

Альтернативная гипотеза сформулирована как «больше» в связи с тем, что в тексте примера указывалось на важность превышения значения критического уровня.

Предположим, что ошибки модели распределены нормально с некоторым математическим ожиданием р и дисперсией а². Стандартное отклонение, рассчитанное по выборке, фактически уже представляет собой сумму квадратов центрированной случайной величины, поэтому для получения величины, распределенной в соответствии с (3.53), нам достаточно каждое значение в выборке разделить на генеральную дисперсию. Однако сами значения нам не даны, но они, в принципе, и не нужны. Из формулы выборочной дисперсии:

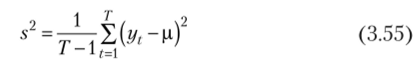
следует, что.

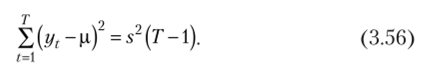
Разделив левую и правую части (3.56) на генеральную дисперсию, получим.

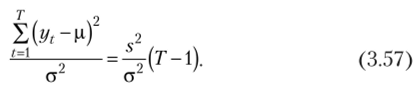
Внесем в левой части формулы (3.57) дисперсию под знак суммы, тогда получим.

В формуле (3.58) в левой части под знаком суммы мы видим стандартную нормально распределенную случайную величину, рассчитываемую по формуле (3.43). Подставим значение из формулы (3.43) в (3.58), чтобы получить.

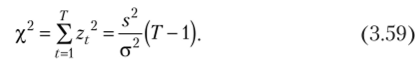
Величина, рассчитанная по формуле (3.59) будет распределена по у}(Т — 1) в том случае, если исходная величинах распределена нормально. Число степеней свободы получилось равным Г — 1 из-за наложения условия (3.55).

Подставим в формулу (3.59) значения из задачи: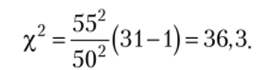

В связи с тем, что в задаче не был указан уровень остаточной вероятности, примем стандартный: а = 0,05. В таком случае табличное значение для %^[1](0,05; 30) составляет примерно 43,8 — это значение соответствует правому хвосту распределения. Сравнивая его с расчетным, приходим к выводу о том, что у нас нет оснований отклонить нулевую гипотезу. Судя по всему, модель можно не переоценивать.

Заметим, что распределение у} в отличие от распределений Гаусса и Стьюдента не симметрично. Поэтому в случае, если потребуется оценить статистики с двух сторон, нам нужно будет отдельно оценить х^[1] —df и у^[3] 1—df, где.

2 ) 12 )

df — число степеней свободы.

В очередной раз обращаем внимание на предположения, лежащие в основе теста: y_t должны быть одинаково и независимо распределенными по нормальному закону величинами.

• [1] учеб, пособие для вузов. 7-е изд. М.: Высшая школа, 2001. С. 147.
• [2] учеб, пособие для вузов. 7-е изд. М.: Высшая школа, 2001. С. 147.
• [3] Гмурман В. Е. Теория вероятностей и математическая статистика :