Предположение о нормальном распределении случайной ошибки в рамках классической линейной регрессии

Проверка гипотез о конкретном значении коэффициентов парной регрессии

В предыдущем параграфе, зная основные числовые значения ошибок, мы нашли основные числовые характеристики для МНК-оценок. Для того чтобы получить информацию о законе распределения этих оценок, необходимо предварительно сделать предположение о распределении ошибок.

Наиболее распространенное предположение, которое делается в рамках классической линейной регрессионной модели, состоит в том, что все ошибки имеют нормальное распределение. Теоретическим обоснованием такого предположения служит центральная предельная теорема (ЦПТ), упоминавшаяся в гл. 2. Напомним, что ошибки в, i = 1,…, п, отражают в парной ре;

л/.

грессии влияние всех остальных факторов, кроме X, т. е. е, = X г'_т. Соглас;

т-1.

но ЦПТ если г¹_т /т независимы и одинаково распределены, то их сумма будет иметь нормальное распределение (вне зависимости от распределения z'_m Vi), если М- достаточно велико. При этом условие ЦПТ об одинаковом распределении параметров может быть несколько ослаблено.

Таким образом, в рамках классической линейной регрессионной модели предположения теоремы Гаусса — Маркова об ошибках усиливаются следующим образом: е,-~ JV (0; a²), г = 1,п.

Утверждение 4.2. Если все ошибки имеют нормальное распределение с нулевым математическим ожиданием и одинаковой дисперсией, т. е. е,.~ N (0; а 1), i = 1,…, п_у то МНК-оценки коэффициентов парной регрессии также имеют нормальное распределение, причем Р₍₎ ~ N (Р₍₎; а^), р, ~ а^).

Доказательство этого утверждения основано на том факте, что линейная комбинация нормально распределенных случайных величин также имеет нормальное распределение.

Зная закон распределения оценок [3₀ и р, мы можем перейти к проверке гипотез. Общая схема такой проверки была описана в гл. 2. Напомним, что все гипотезы формулируются парами: основная гипотеза Я₀ и альтернативная гипотеза Я,.

Начнем с проверки гипотез о конкретном значении коэффициента наклона (для свободного члена все результаты аналогичны). Основная гипотеза имеет следующий вид:

где Pj — конкретное число, например 0 или 5.

Альтернативная гипотеза может быть двусторонней: Я: р, ^ ру или одной из односторонних: Я: p_t > ру или Я₁: p_t < ру.

При выборе тестовой статистики используются следующие соображения: если гипотеза Я₀: Pj = РУ не отвергается, то p_t ~ N (р,; ajj).

Pi — РУ Тогда статистика z =-имеет распределение A^r(0; 1). К сожалению,.

^аР, в выражение для входит неизвестный параметр о²_еУ поэтому вычислить эту статистику невозможно. Традиционный прием в таких случаях — замена неизвестного параметра а² его оценкой а², но в этом случае распределение статистики z уже не будет нормальным.

Выясним, каким же будет распределение статистики ————. Для этого.

1 °*.

воспользуемся следующими утверждениями¹.

Утверждение 4.3. &² = является несмещенной оценкой параметра a² дисперсии ошибок.

ж, ^ «RSS

Утверждение 4.4. Величина —— для парной регрессии имеет распределение у?_п_₂.

Утверждение 4.5. Оценки (3, иа_е² независимы.

Замечание 4.1. Оценки стандартных ошибок оценок коэффициентов регрессии р_о и Pj вычисляются по формулам.

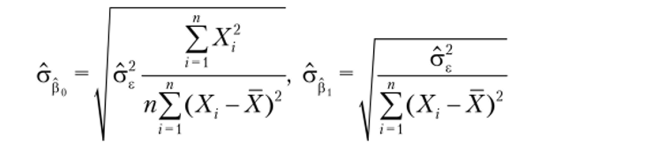
и выдаются статистическими пакетами при оценке параметров регрессии.

Проведем некоторые преобразования статистики^, в результате.

^ае, которых выявим ее закон распределения:

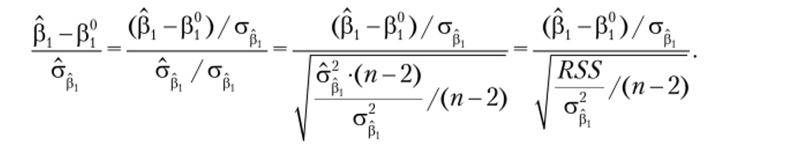
п ?? — Р?

Поскольку случайная величина —i-имеет стандартное нормальное.

^аР,.

RSS

распределение, а случайная величина —— — распределение %1 ₂ ^{и эти СЛ}У" .

^aPi.

чайные величины независимы (см. утверждение 4.5), то случайная величина —~ имеет распределение Стьюдента с (п — 2) степенями свободы.

^aPi.

(см. определение 2.31).

Мы можем вернуться к проверке гипотезы о конкретном значении коэффициента наклона. Начнем с процедуры выбора между Н₀ и Н_{ при двусторонней альтернативной гипотезе и уровне значимости а:

_п ", Р.-э?

В первую очередь вычисляем значение тестовой статистики t = —~-.

^aPi.

Если это значение является «слишком большим», а именно, если > tffin — 2), то гипотеза Н₀ отвергается в пользу гипотезы H_vГрафически это можно изобразить следующим образом (рис. 4.1).

Если значение тестовой статистики попадает в заштрихованную область, то гипотеза Н₀ отвергается. В противном случае (а именно, если И ^ *а/г (^и «2), т. е. t попадает в незаштрихованную область) гипотеза Я₍₎ не отвергается.

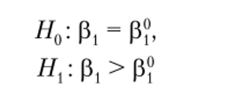
Аналогично проверяются и односторонние гипотезы. При выборе между гипотезами.

Рис. 4.1. Критические области нормального распределения.

р. — э? .

тестовая статистика t = —;-не изменяется, а правило выоора между ги;

потезами выглядит следующим образом: если t > t™^l(n — 2) (это соответствует попаданию тестовой статистики в заштрихованную область на рис. 4.2), то гипотеза Н₀ отвергается в пользу альтернативной.

В последнем случае неравенства меняются на противоположные. При выборе между гипотезами.

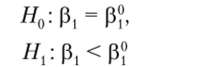
р,-р?

тестовая статистика t = —-по-прежнему не меняется, а правило при;

^аР.

нятия решений принимает следующий вид: если t < - 2) (в этом случае это соответствует попаданию тестовой статистики в заштрихованную область на рис. 4.3), то гипотеза Н₀ отвергается в пользу альтернативной.

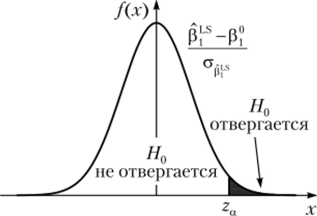
Рис. 4.2. Правый хвост Рис. 4.3. Левый хвост нормального распределения нормального распределения.