Решение задач динамики методом конечных элементов

Метод конечных элементов (МКЭ) относится к приближенным методам. При его использовании реальная система с бесконечным числом степеней свободы заменяется системой с конечным числом степеней свободы. Замена распределенной массы узловой производится отдельно для каждого элемента, но не, но правилу рычага, а из условия равенства возможных работ сосредоточенных и распределенных сил инерции. Более полно с МКЭ можно ознакомиться по книге [15] или по другим источникам, посвященным ему^[1]. В настоящем издании приводятся только матрицы, необходимые для решения рассматриваемых задач.

Как известно, в МКЭ большей частью реализуются идеи метода перемещений. Основная система метода перемещений, как правило, состоит из двух типов стержней (рис. 4.8). Примем эти прямолинейные стержни постоянной жесткости EI с равномерно распределенной массой т за отдельные конечные элементы. Первый стержень (рис. 4.8, а) имеет четыре степени свободы, включая перемещения стержня как твердого тела, второй — три.

Рис. 4.8. Типы конечных элементов, составляющих основную систему.

метода перемещений Для первого стержня принята функция перемещений Y = /, + f^x + /^т²+ + /₄:г³, а для второго у = f_{ + + f^x³.

На основе этих функций получаем соответствующие матрицы жесткости и матрицы эквивалентных масс:

Уравнение (2.8), приведенное в гл. 2, можно использовать и при решении задач методом перемещений. В этом определителе.

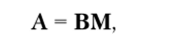
где В — матрица податливости всей системы.

Заменим ее матрицей жесткости: В = К *. Тогда уравнение (2.8) примет вид.

Это же уравнение можно записать по-иному, если матрицу, определитель.

от которой берется, умножить слева на матрицу К и разделить на X_j = —:

В любом случае для определения частот свободных колебаний необходимо вычислить матрицы К и М. Они обе вычисляются по аналогичным формулам:

Матрицы r_g и М^для каждого элемента приведены в формулах (4.17)—(4.19). При составлении матрицы масс для всей конструкции следует помнить, что в свободных рамах имеет место перенос массы стержней вдоль их оси как твердого тела. Этот факт нужно учитывать путем добавления переносимой массы к соответствующим элементам матрицы, определяемой по формуле (4.23).

Пример 4.6. Определим частоты свободных колебаний рамы, представленной на рис. 4.9, а.

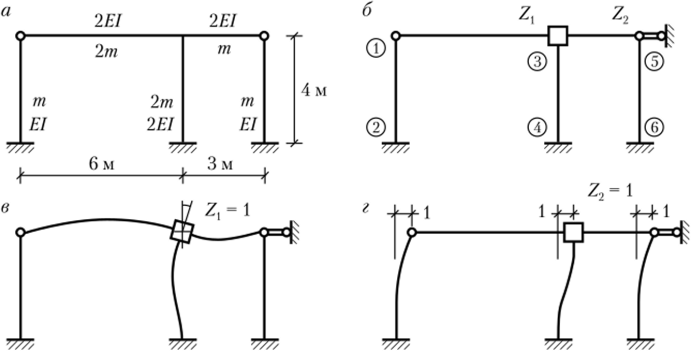
Рис. 4.9. Расчет рамы методом перемещений.

Решение

За конечные элементы примем отдельные стержни. В результате число степеней свободы будет равно двум.

Основная система метода показана на рис. 4.9, б (в кружках приведены номера узлов). Составим матрицы жесткости и масс стержней:

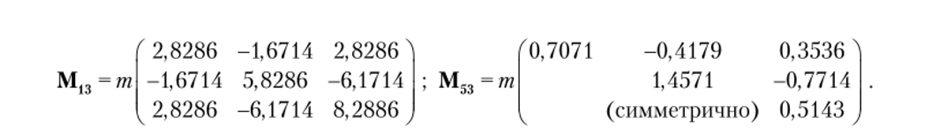
В данном примере рама свободная. При перемещении по направлению Z₂ стержни 1−3 и 3−5 перемещаются как твердое тело без деформирования. Чтобы учесть смещение их массы, составим специальную матрицу М_т. В ней будет только один ненулевой член:

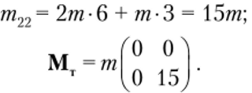
Далее составим для каждого стержня матрицы преобразования перемещений по рис. 4.8, в, г:

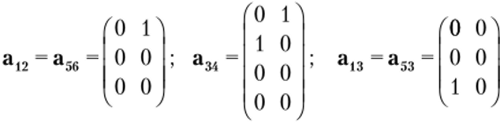
Вычисления выполним по формуле (4.20) с помощью системы MATLAB в такой последовательности:

Упражнение 4.6. Для рамы, изображенной на рис. 4.10, определите частоты свободных колебаний, соответствующие кососимметричным формам колебаний. С этой целью рекомендуется использовать симметрию рамы и принять групповое неизвестное для углов поворота. Числовые данные к задаче: /=6м;? = 20- 10⁶кН/м²; I = 1,44−10 ⁴ м⁴; т = 3 т.

В результате вычислений получаются следующие матрицы:

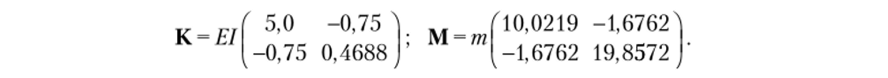
Частоты собственных колебаний:

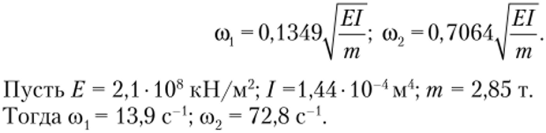
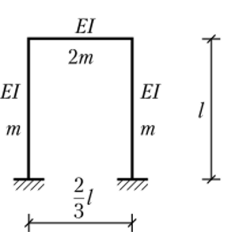
Рис. 4.10. Симметричная рама.

В случае расчета на вибрационную нагрузку удобнее воспользоваться выражением для матриц тина использумого в уравнении (4.21), заменив в нем сона 0 — угловую частоту возмущающей нагрузки. Уравнения метода примут вид.

где матрица жесткости всей системы К и матрица масс М по-прежнему определяются по формулам (4.22) и (4.23); R₍₎ — матрица реакций в дополнительных связях от внешней нагрузки; 0 — нулевая матрица. Усилия определяются отдельно для каждого стержня по выражению.

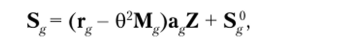
где S,!¹ — матрица усилий в расчетных сечениях стержня от неузловой нагрузки.

Пример 4.7. Чтобы оценить возможности МКЭ, выполним расчет рамы, приведенной в примере 2.6 (рис. 4.11, а). Основная система метода перемеще;

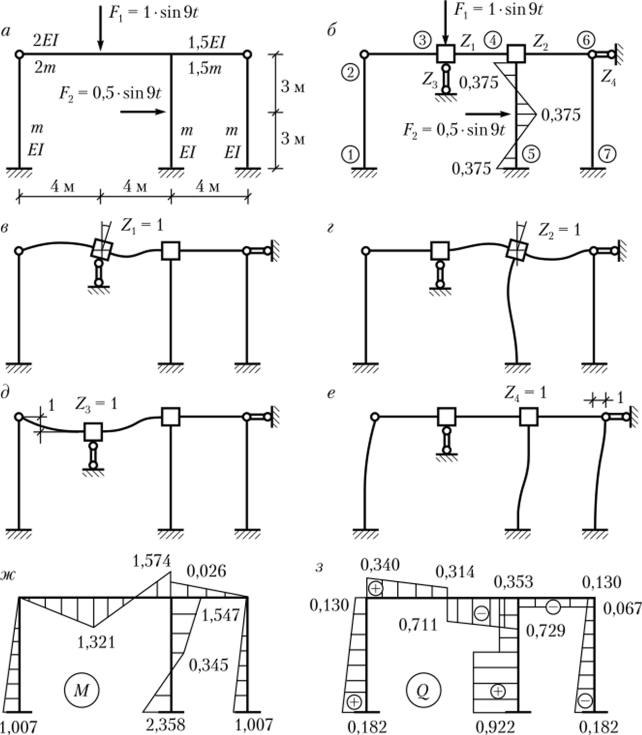
Рис. 4.11. Расчет рамы на вибрационную нагрузку МКЭ ний показана на рис. 4.11, 6. Там же показана эпюра от внешней нагрузки. При выбранной основной системе имеют место четыре степени свободы. На рис. 4.11, в — е приведены схемы деформаций от единичных перемещений по направлению добавленных связей.

Решение

Составим исходные матрицы:

Дальнейшие вычисления выполним с помощью системы MATLAB. Процедура вычислений приведена в приложении 1.3.

Получаем следующие значения частот свободных колебаний:

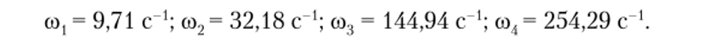
К частотам, полученным в примере 2.6, оказалась близкой только низшая частота. Расхождение объясняется различными подходами к замене распределенной массы сосредоточенными. Па рис. 4.11, ж, з приведены эпюра изгибающих моментов и эпюра поперечных сил. Значения усилий оказались отличными от результатов примера 2.6.

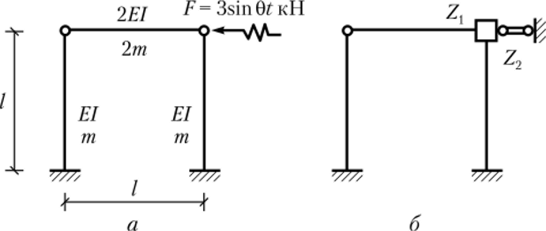
Рис. 4.12. Рама с двумя степенями свободы для приведенной основной системы Упражнение 4.7. Определите частоты свободных колебаний и постройте эпюры изгибающих моментов и поперечных сил для рамы, изображенной на рис. 4.12, а. Основную систему выберите, как показано на рис. 4.12, 6. Угло;

. «а 1,584 Щ

вая частота вынужденных колебании равна 9 = —-р—J—•.

Контрольные вопросы

• 1. Каково определение потенциальной энергии?
• 2. Чему равна потенциальная энергия?
• 3. Какой закон реализуется при колебании без учета диссипативных сил при создании энергетического метода определения частоты свободных колебаний?
• 4. Чем нужно задаваться при использовании энергетического метода?
• 5. Является ли энергетический метод точным?
• 6. Нужно ли заменять распределенную массу сосредоточенной при использовании энергетического метода?
• 7. Можно ли использовать энергетический метод, если сечения стержней переменные и масса распределена неравномерно?
• 8. В чем заключается способ приведенных масс?
• 9. Метод конечных элементов при решении задач динамики является точным или приближенным?

• [1] См., например, книгу: Ильин В. П., Карпов В. В., Масленников А. М. Численные методырешения задач строительной механики. М.; СПб., 2005.