Статистические гипотезы и критерии их оцепки в задачах оценки рисков

Предположение о том, что рассматриваемая случайная величина подчиняется определенному закону распределения, будем называть статистической гипотезой. Оценка соответствия интересующей экспериментатора статистической гипотезы имеющимся данным производится путем применения определенного правила, зависящего от характера выдвинутой гипотезы и называемого статистическим критерием. Статистический критерий представляет собой стандартный прием оценки соответствия выдвинутой гипотезы эмпирическим данным. Следует отметить, что признание удовлетворительности согласия анализируемой гипотезы с экспериментом, устанавливаемое при помощи соответствующего критерия, отнюдь не эквивалентно доказательству се справедливости. Такое признание означает лишь, что полученные в ходе наблюдений за некоторой случайной величиной данные не противоречат проверяемой гипотезе. В соответствии с этим принятие гипотезы можно рассматривать как указание на то, что гипотеза может служить рабочей по крайней мере до тех пор, пока в распоряжении аналитика не окажутся новые данные, которые могут внести коррективы в интерпретацию результатов наблюдений.

Пусть в нашем распоряжении имеется величина х₀ — одно из возможных значений некоторой случайной величины X. Выдвинем гипотезу, которую обозначим Я₀, о том, что случайная величина X распределена по закону, характеризуемому заданной функцией плотности вероятности <�р₀(х). Гипотезу Я_(| назовем нуль-гипотезой. Введем также некую альтернативную гипотезу Н, содержание которой состоит в том, что рассматриваемая случайная величина X подчиняется закону распределения, описываемому функцией плотности вероятности cpi (x), и будем считать, что гипотеза //, является истинной, если нуль-гипотеза Я₀ неверна. (Ввиду того, что вид функции q>| (эс) обычно неизвестен, то чаще всего ее наличие подразумевают лишь неявно.) Требуется на основании величины.

*о решить, какой из гипотез — Я0 или Я| — следует отдать предпочтение.

Критерий оценки статистической гипотезы (т. е. правило для ее принятия или отвержения) проще всего получить, если предположить, что проверяемая гипотеза Я0 верна, т. е. рассматриваемая случайная величина действительно распределена по закону, задаваемому функцией 0(лг), и рассмотреть область, в которой оказалось наблюдаемое значение х0. Пусть х0 попало в область, расположенную вблизи правого (рис. 2.2) или левого хвоста функции Фо (х), и, следовательно, вероятность попадания случайной величины в эту область, вычисленная при помощи функции 0 неверна. Практика применения теории проверки статистических гипотез показывает, что в этой ситуации целесообразно выбрать альтернативу, т. е. признать ошибочность гипотезы Я0.

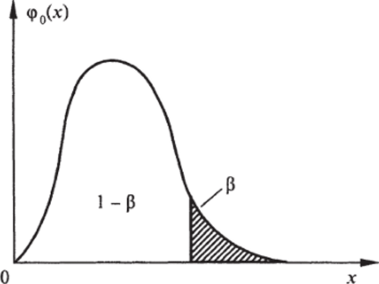
Рис. 2.2. Критическая область функции распределения случайной величины Наоборот, если наблюдавшееся значение х0 оказалось в интервале, достаточно удаленном от обоих хвостов функции фо (х), то целесообразно считать, что гипотеза Я0 может быть принята. Интервал значений случайной величины (отрезок оси абсцисс), расположенный вблизи хвоста функции.

критическую область свидетельствует о неприемлемости анализируемой гипотезы. Вероятность попадания случайной величины в критическую область (которая может состоять только из одной части, расположенной у правого или левого хвоста функции Фо (х), либо из обеих частей одновременно) получила наименование уровня значимости. Для правостороннего критерия (рис. 2.2) эта вероятность есть площадь заштрихованной области, т. е.

Если вероятностью р (т. е. уровнем значимости) мы задаемся заранее, то по уравнению (2.23) (или аналогичному для левостороннего и двухстороннего критериев) устанавливают значение хр, определяющее правило принятия или отвержения гипотезы Н₀.

Таким образом, искомый статистический критерий оценки гипотезы Н₀ состоит в сравнении х₀ с численной величиной хр. Если (в предположении правостороннего критерия).

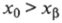
для выбранного уровня значимости р, то х₀ попадает в критическую область постулируемой функции распределения и нуль-гипотеза Но должна быть отброшена. Если же.

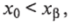
то х₀ лежит вне критической области и гипотеза Но может быть принята.

Итак, задача построения критерия оценки гипотезы Н₀ на основе известного значения х₀ случайной величины X и постулируемой функции фо (х) может быть решена, если задаться величиной уровня значимости Р критерия, определяющего размеры критической области функции ф₀(х). Нетрудно убедиться, что уровень значимости по определению совпадает с вероятностью отвергнуть проверяемую гипотезу Я₀, когда она в действительности верна. Поэтому выбор, например, 1% -ного уровня значимости означает, что только в одном случае применения критерия из ста верная в действительности гипотеза будет отвергнута. Отсюда, на первый взгляд, кажется, что необходимо всегда стремиться задавать возможно более низкое значение уровня значимости. Однако это не так. Уменьшение значения уровня значимости ведет к одновременному уменьшению вероятности отвергнуть гипотезу Hq, когда она является ложной. Таким образом, стремление чрезмерно обезопасить себя от браковки правильной в действительности гипотезы может повлечь за собой нежелательное снижение чувствительности используемого критерия по отношению к ложной гипотезе.

Компромисс между вероятностями отвергнуть верную и неверную в действительности гипотезы обеспечивается, если при выборе уровня значимости руководствоваться определенными рекомендациями, выработанными практикой применения статистических гипотез.

Принятие гипотезы. Если проверяемая гипотеза принимается с 5%-ным или более высоким значением уровня значимости, то гипотезу, безусловно, следует признать согласующейся с полученными экспериментальными данными.

Если проверяемая гипотеза может быть принята с уровнем значимости, меньшим 5%-ного, но большим 1%-ного, то можно либо пойти на риск принятия гипотезы, либо взять гипотезу под сомнение. В такой ситуации следует признать целесообразным провести повторный эксперимент для получения данных, на основании которых можно было бы сделать более определенные выводы.

Применения критерия с более низким, чем 1%-ным, значением уровня значимости для принятия гипотезы следует избегать.

Отбрасывание гипотезы. Если гипотеза отвергается с 1%-ным или более низким значением уровня значимости, то гипотезу, безусловно, следует признать не согласующейся с полученными экспериментальными данными.

Если проверяемая гипотеза может быть отвергнута применением более высокого уровня значимости, лежащего между 1%-ным и 5%-ным значениями, то гипотезу либо также следует отвергнуть, либо только поставить под сомнение и, повторив эксперимент, вновь оценить выдвинутую гипотезу.

Применение 5%-ного или более высокого значения уровня значимости не дает оснований для отбрасывания гипотезы.

Гипотеза, формулируемая для статистической проверки, может относиться к параметрам предполагаемого распределения генеральной совокупности (например, к среднему р или дисперсии о² нормального распределения). Критерий для проверки такой гипотезы о параметрах называется параметрическим критерием. Однако не всегда можно сказать заранее, какая именно функция распределения имеет место. Поэтому были разработаны методы проверки, позволяющие сравнить распределения, не зная их параметров или формы. Такие критерии, основанные на сравнении функций распределения (а не параметров), называются пепараметрическими критериями. Они имеют определенные преимущества по сравнению с параметрическими благодаря меньшим требованиям к их применению, большему диапазону возможностей и часто большей простоте реализации. Конечно, нужно считаться и с более низкой точностью этих критериев по сравнению с параметрическими.

Результаты статистических методов проверки часто бывают неудобны для аналитиков. Во многих случаях они дают незначимые (Р₀ < 0,95) или спорные (0,95 < Р₀ < 0,99) различия, хотя на основе субъективного опыта уже установлено «истинное» различие. В подобных случаях часто помогают дополнительные измерения (повторные наблюдения). Чем больше получено результатов, тем меньшие различия будут достоверно фиксироваться. Ни в коем случае нельзя соблазняться заменой точных данных сомнительными, т. е. на основании субъективной оценки.

Распределение Стьюдента и оценка риска по существенности различий в выборочных данных В предыдущем изложении мы уже отмечали, что нормальность закона распределения показателя, по которому оценивается риск, чаще всего постулируется, т. е. принимается соответствующей истине без доказательства. Основываясь на этом, интервал, в котором изменяется показатель, считают равным 2о (т. е. говорят, что «…с вероятностью 0,95 случайная величина заключена в интервале…»). Именно величина 2о определяет вероятность, равную 0,95. Однако в действительности генеральная дисперсия а² (х) остается неизвестной. Поэтому неизвестна и мера допускаемой ошибки прогноза даже при верности допущения о нормальности распределения избранного показателя риска, т. е. относительная величина U = -——. Для больших п можно полагать sx) = о² (х) и прио (х) менение изложенного математического аппарата будет закономер;

" х-п ным. В противном же случае величина t = —— может значительно.

s (x)

отклоняться от значения U, а, значит, интервал, в котором заключена случайная величина X, с той же вероятностью 0,95 будет резко отличаться от вычисляемого.

Распределение случайной величины, аналогичной U, в котором вместо генерального среднеквадратического отклонения стоит соответствующее выборочное отклонение, т. е.

впервые было введено Стьюдентом (псевдоним английского химика Госсета) и носит название распределения Стьюдента.

Функция плотности вероятности величины / определяется числом /степеней свободы выборочной дисперсии s² (х).

При значениях/ > 20 функция распределения Стьюдента удовлетворительно аппроксимируется функцией нормального распределения. Поэтому уже с числа наблюдений более 20 обычно для вычисления величин доверительных интервалов и ошибок используют нормальный закон. При небольшом же числе измерений (а, значит, и числе степеней свободы) распределение Стьюдента существенно отличается от нормального. В этом случае интервал, в котором с некой вероятностью заключена исследуемая величина, рассчитывают не по таблицам Гаусса, а по таблицам /-распределения (приложение 2).

Если вероятность, а для случайной величины / попасть в какойлибо интервал задана, то границы искомого интервала будут характеризоваться величинами -t-_a(f) и /] _а(/), зависящими от числа степеней свободы / и определяемыми из условия.

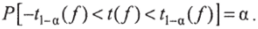
Пример. Найти величину интервала, для которого вероятность попадания случайной величины I, имеющей одну степень свободы, равна 0,95.

Имеем, а = 0,95, 1 — а = 0,05,/ = 1. При помощи приложения 2 находим г₀05 (1) ⁼ 12,706. Отсюда искомый интервал есть (-12,706; + 12,706).

На практике риск финансовой операции всегда оценивают не по абстрактной совокупности всех возможных сделок, а по конкретным и уже имевшим место в сходных условиях аналогам.

Предположим, что с целью оценки риска финансовой операции по приобретению ценных бумаг зафиксированы данные о продажах двух видов бумаг в течение небольшого периода (по п сделок с каждым видом). Получены_следующие результаты: средние уровни стоимости продаж Х и Х₂ и исправленные средние квадратические отклонения s и s₂. Как установить, является ли расхождение l-^i — Х₂ случайным или оно обусловлено тем, что одна из бумаг более предпочтительна на фондовом рынке, а, следовательно, и менее рискованна?

Следует иметь в виду, что ответ на данный вопрос не может быть строго определенным, он либо будет верен с некоторой вероятностью q, либо ошибочен с вероятностью р = 1 — q, называемой, как мы уже отмечали, уровнем значимости.

Составим случайную величину.

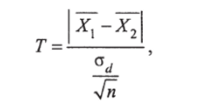
где п — объем выборки. Доказано, что данная случайная величина подчиняется /-распределению Стыодента.

Случайная величина Т зависит от числа степеней свободы /= 2(л — 1) и уровня значимости р. По заданному р и числу степеней /определяется t теоретическое в таблицах распределения Стыодента (приложение 2).

По формуле для Т находят I практическое, отвечающее изучаемой ситуации:

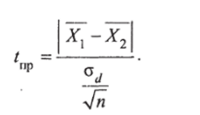
Если ?пр < /_теор, то с вероятностью ошибки, равной р, считают, что расхождение между средними незначимо, и различие в риске приобретения бумаг существенным признать нельзя. Если /_пр > 7_{Т (}._ор, то расхождение между средними выборочными существенно, и с доверительной вероятностью у = 1 -р можно утверждать, что сделка по одной бумаге будет менее выгодной, чем по другой.

Если объем выборочных совокупностей неодинаков, то используют более сложные формулы, которые можно найти в подробных курсах математической статистики.

Зачастую, однако, финансовый менеджер вынужден оценивать риск финансовых операций не по устоявшимся одиночным показателям, а по тенденциям, имеющим место на рынке (по динамическим рядам).

Динамическим рядом называют последовательность наблюдений одного показателя, упорядоченную в соответствии с возрастанием или убыванием другого показателя. Если упорядочение осуществляется по времени, то такой динамический ряд называется временным рядом. Элементы ряда принято называть уровнями. При существовании тенденции во временном ряду говорят, что он имеет тренд, т. е. изменение, определяющее общее направление развития.

Пусть даны два динамических ряда:

и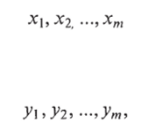

полученных независимо друг от друга. Каждыйу'-й член ряда (xj и у.) принадлежит одному и тому же периоду времени и отражает собой некий параметр финансовой операции (например, доходность). Нужно выяснить, есть ли разница между динамическими рядами, чтобы оценить рискованность бизнеса в соответствующих сферах.

Если оба ряда одинаковы, то разности dj = yj — Xj будут беспорядочно рассеиваться вокруг нулевого значения. Следовательно, для принятия решения необходимо проверить гипотезу о равенстве нулю средней разности, точнее, принадлежит ли средняя.

— x±^d /

разность d = 2_, / генеральной совокупности с параметром y=i ^/т

p_rf=0. Получается следующая схема расчета («расширенный /-критерий»):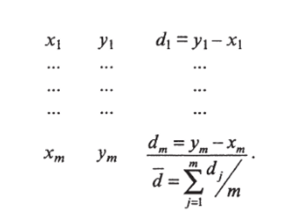

Значимость отклонения средней разности d от ожидаемого значения, равного нулю, проверяется в соответствии с уравнениями распределения Стьюдента по квантилю и дисперсии

с/= т — 1 степенями свободы.

Сравнение проводят обычным способом по процентным точкам /-распределения. При / > / (Po, f), где Ро— доверительная вероятность в 0,95, можно констатировать разницу между рядами наблюдений, а, следовательно, и в тенденциях.

Пример. Для принятия решения об инвестировании в одну из отраслей определяли ставку маржинального дохода в первой (х) и второй (у) отраслях. Необходимо установить, существенна ли разница между отраслями в тенденциях доходности.

Исходные данные и промежуточные расчеты сведены в таблицу.

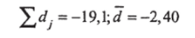
Расчет дисперсии разности дает величину s_d = 2,32 при/= 7 степенях свободы.

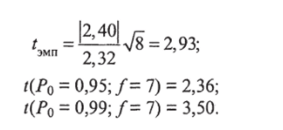
Так как t (P₀ = 0,95; f) < /_эмп < t (P₀ = 0,99; Д между тенденциями доходности в отраслях существует статистически значимая разница и инвестировать целесообразнее в отрасль х.

X^распределение

Пусть имеется п независимых случайных величин Х, Х₂, …Х_п, каждая из которых подчиняется нормальному закону распределения с параметрами рис. Для каждой случайной величины составим выражение.

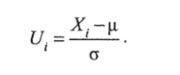
Тогда сумма квадратов случайных величин f} ~ имеет закон распределения, называемый Х²-распределением с/= п степенями свободы.

Из того, что величина X² образуется как сумма квадратов, видно, что она связана с дисперсией некоторой случайной величины. Таблица Х²-распределения представлена в приложении 3. Основное назначение Х-критерия — сравнение теоретических и эмпирических распределений.

Пусть имеется ряд из п наблюдений за некоторым показателем риска. Необходимо установить, можно ли описать эти п значений с помощью принятого теоретического распределения (модели оценки риска). Для проверки выдвигают нулевую гипотезу о том, что между эмпирическим распределением и теоретической моделью нет никакого различия. Из п значений в выборке наблюдений (и > 50) вычисляют среднее р и стандартное отклонение ст, а затем разбивают п значений на т~-/п классов. Для каждого полученного класса определяют абсолютную частоту (т. е. число) А попавших в него значений и сопоставляют ее с частотой, А «теоретически ожидаемой в соответствии с моделью. Для разных теоретических распределений частоты протабулированы при о = 1. Поэтому прежде всего для сравнения стандартизируют наблюдения в классах по формуле U = (х — р)/о. Для таких нормированных значений в таблице распределения Гаусса находят соответствующие им значения функции. Принимая во внимание число измерений и, ширину класса d и стандартное отклонение о, вычисляют теоретически ожидаемые абсолютные частоты h, попадания в отдельные классы. Из эмпирических и теоретических частот составляют выражение.

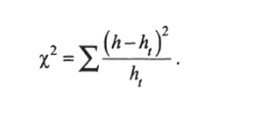
Если теоретические значения h, для отдельных классов достаточно велики (h, > 5), то найденное выражение будет следовать Х²-распределению с/= т — к степенями свободы. При этом к представляет число параметров, необходимых для описания выборки. Для нормального (Гауссова) распределения к = 3 (среднее х, стандартное отклонение s и объем выборки л), для распределения Пуассона к = 2 (среднее х и объем выборки л).Требуемое для отдельных классов значение h, > 5 можно получить, объединяя несколько соседних классов. Если при проверке получается, что X² > X² (ЛУ), то проверяемая гипотеза отбрасывается; между эмпирическим и теоретическим распределением существует значимое различие. Различие незначимо, если X² < X² (P, J) —