Особенности моделирования систем

При моделировании сколько-нибудь сложных социальных систем необходимо учитывать ряд важных понятий.

Неравновесное состояние системы — состояние, при котором в системе происходит или может в любой момент начаться одностороннее изменение ее параметров. Из данного определения нетрудно заключить, что в случае равновесия имеют место либо стабильные, либо циклически меняющиеся значения параметров. При этом вводится понятие равновесных процессов — процессов, при которых система последовательно переходит из одного состояния равновесия в другое.

В случае если моделируются противодействия и противоречия, часто состояние равновесия является компромиссным состоянием для сторон с конфликтующими интересами. Яркий пример из социально-экономической сферы — понятие равновесной цены (рис. 10.2). Очевидно, что при установлении цены ниже равновесной продавцам будет невыгоден сбыт товара, а при установлении цены выше равновесной покупателям будет невыгодно приобретение товара.

Пример

Также равновесные состояния часто возникают в процессе военных конфликтов, когда ни одна из сторон не в силах «сдвинуть» ситуацию в свою пользу. Например, такими ситуациями были «Верденская мясорубка» (1916 г.), оборонительный этап Сталинградской битвы (август — октябрь 1942 г.) или «патовая ситуация» в ходе войны в Ливии (весна 2011 г.). Эти случаи — наиболее реальные возможности договориться без унизительных условий для какой-то стороны и тем более полного истребления одной из сторон. Также равновесные состояния хорошо знакомы шахматистам: играющим в шахматы достаточно вспомнить любую позицию, когда и они, и соперник охотно завершали партию вничью.

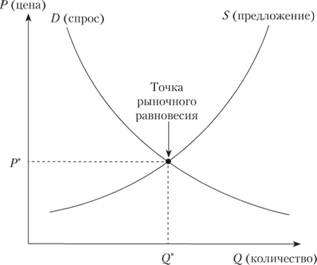
Рис. 10.2. Классический пример равновесного состояния.

Система устойчива, если при выведении ее из состояния равновесия внешними воздействиями она возвращается в него после прекращения внешних воздействий. Если же она не возвращается к состоянию равновесия, то система неустойчива. Реальные системы не могут быть устойчивы при абсолютно любых воздействиях, но могут быть устойчивы в некоторых пределах. Например, политическая система жизни общества в стране не «расшатается» при некотором воздействии иностранной пропаганды, ведущейся с целью сменить режим, но при более сильном воздействии она «расшатается» .

Рассмотрим важнейшее понятие " точка бифуркации"  — это смена установившегося режима функционирования системы. Точка бифуркации носит кратковременный характер и разделяет более длительные периоды устойчивого функционирования системы. Основное свойство точки бифуркации — непредсказуемость: система может пойти по одному из путей, перейдя к одному из нескольких возможных устойчивых режимов функционирования, но, как правило, нельзя предсказать, к какому конкретно режиму. Иными словами, малая случайность может направить систему как по благополучному пути развития, так и по катастрофическому.

Пример

При попытке государственного переворота существуют как минимум три варианта:

• 1) быстрая смена режима (как в случае большинства «цветных революций» XXI в.);
• 2) переход в состояние затяжной борьбы (как, например, произошло в 2011 г. в Ливии и Сирии или после ухода советских войск из Афганистана);
• 3) подавление мятежа и сохранение действующего режима (как, например, в случае Андижанского мятежа 2005 г.).

В точке бифуркации проще всего вмешаться в ход развития системы, повернув ее развитие в сторону, в которую ее заинтересован направить воздействующий субъект. Недаром практически всегда, как только в некоторой стране обостряется политическая ситуация, оказывается, что одну из сторон поддерживают зарубежные силы или местные олигархи. Чтобы перевести систему в «желательный» режим функционирования из устойчивого режима функционирования, нужно гораздо больше усилий. Требуется «столкнуть» систему в неустойчивое состояние и затем повлиять на выбор ею нового устойчивого режима.

Процессы, происходящие в системах, могут быть обратимыми и необратимыми. Процесс Р называется необратимым, если его можно провести только в одну сторону. Попытка выполнить над системой те же операции, что и при процессе Р, но в противоположном порядке, либо невозможна, либо не вернет систему в исходной состояние. Некоторые процессы можно «повернуть вспять» на начальных этапах, но с некоторого момента это сделать нельзя. Точка, после которой процесс необратим, называется точкой невозврата. После перехода через точку невозврата система уже не может быть прежней. Исторический пример точки невозврата для системы «политическая жизнь в Европе» — 22 июня 1941 г. Чем бы ни окончилась начавшаяся в тот день война, политическая ситуация в Европе все равно кардинально изменилась бы по сравнению с 1920—1930;ми гг.

При моделировании реальных систем почти всегда необходимо исследование на точки равновесия, бифуркации, невозврата, а также анализ устойчивости.

Нелинейность систем. Также крайне важно учесть, что практически все реальные системы обладают нелинейными свойствами в той или иной степени. В ряде случаев, однако, влияние нелинейности может быть пренебрежимо мало, тогда для описания системы можно пользоваться упрощенными линейными моделями. При выборе модели описания движения системы необходимо располагать информацией, как скажется на характеристиках состояния системы влияние нелинейных связей.

Очень часто нелинейные системы характеризуются квадратичными уравнениями. Квадратичная компонента — простейший способ учесть связи элементов системы, которые и дают нелинейность, создавая различие между совокупным действием элементов системы и простой суммой действий элементов.

Пусть элементы системы кооперируются для некоторого совместного действия. Простейшая модель следующая. Пусть есть двухэлементная система и ресурс каждого элемента равен x. Чем «сильнее» каждый элемент и чем интенсивнее их связь, тем больше эффект от этой связи. Получим, что эффект от разрозненного действия составил бы 2х, а эффект от совокупного действия составит 2х + bх2, где b — интенсивность связи. Аналогичную квадратичную модель можно составить для произвольного числа элементов в системе, где каждый элемент связан с каждым.

Пример

Вероятно, именно системным эффектом были обусловлены слова, приписываемые Наполеону: «Два мамлюка безусловно превосходили трех французов; 100 мамлюков были равны по силе 100 французам; 300 французов обычно одерживали верх над 300 мамлюками, а 1000 французов всегда побивали 1500 мамлюков»^[1]. Получается, что х-коэффициент был существенно выше у мамлюков, но Л-коэффициент был существенно выше у французов.

Также достаточно частой ситуацией при моделировании систем является появление дифференциальных уравнений с параболой в правой части. Кроме упомянутой модели Налимова, знаменитой квадратичной моделью является одна из моделей взрывного роста численности населения планеты. По словам С. П. Капицы, «Секрет… взрывного развития состоит в том, что скорость роста пропорциональна квадрату численности населения мира». Соответствующее уравнение основано на представлении о коллективном взаимодействии и имеет вид^[2]

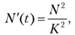
где К — константа, N — численность населения Земли.

Также упоминание заслуживает уравнение логистического роста:

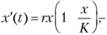
где х — показатель развития (например, численность популяции, богатство участника экономического сообщества), К — параметр, ограничивающий рост, r — начальный темп роста. Логистическое уравнение обладает двумя важными свойствами. При малых значениях х численность возрастает экспоненциально, при больших — приближается к пределу К.

Например, применительно к оценке эффективности инвестиций данное уравнение показывает ограниченный предел богатства даже при самом благоприятном варианте развития инвестиционного цикла. В качестве параметра К выступает параметр пределов роста, характеризующий потенциал роста от начального богатства до предельно достижимого^[3].

Решением уравнения логистического роста является логистическая кривая. На рис. 10.3 приведен вид кривой при r = К = 1, х(0) = 0,5.

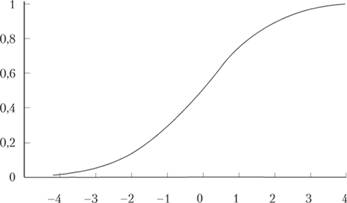
Рис. 10.3. Логистическая функция.

Статические и динамические системы. При моделировании системы принципиально знать, к какому из двух названных классов следует отнести систему. Динамическая система — система, которая изменяется во времени. Статическая система — система, которая на изучаемом отрезке времени может рассматриваться как постоянная. При этом неверно проводить строгое соответствие одноименным классам моделей. Статические модели могут описывать как статические системы, что естественно, так и динамические системы — путем характеристики их состояния в заданный момент. Статическая модель рассматривает «снимок» динамической системы в заданным момент.

Пример математического моделирования

Рассмотрим пример из социально-экономической сферы — процесс математического моделирования государственного долга перед населением. Пусть х — текущий государственный долг, меняющийся со временем t. В нашей модели скорость его прироста будет складываться из двух составляющих:

• 1) а — чистый денежный ноток, направленный от населения (включая юридических лиц);
• 2) процентные начисления при процентной ставке г.

Скорость прироста по второй составляющей прямо пропорциональна текущему долгу, скорость прироста по первой составляющей считаем неизменной. В результате получим следующее уравнение:

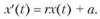
Данная модель является линейной, поскольку описана линейным дифференциальным уравнением. Также она является динамической, поскольку описывает изменение количественной характеристики — долга х — во времени. Кроме того, она детерминированная, поскольку однозначно описывает зависимость параметра х от параметра t. Параметр I является независимой переменной, а х — функцией от него, поэтому модель является функциональной.

При неизменной ставке r? 0 получим следующее решение дифференциального уравнения:

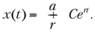
Строго говоря, получено семейство решений, задаваемой произвольной постоянной С, которая может принимать любое действительное значение. Пусть в начальный момент времени долг составлял А, тогда, подставив в решение? = 0, получим:

При r = 0 уравнение вырождается в x'(t) = я, тогда х(t) = at + С. Аналогично предыдущему случаю, вводим дополнительное условие х(0) = А и получаем х(t) = at + А.

На рис. 10.4 показано, как выглядят полученные решения графически. Здесь видно, что при сколько-нибудь существенной процентной ставке процентные начисления становятся очень важной составляющей.

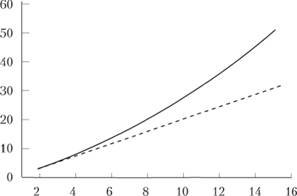
Рис. 10.4. Графики зависимости государственного долга от времени:

- r = 0,06; а = 2; А = 3;  — r = 0;a = 2; А = 3.

Возможно и построение более точных моделей, учитывающих инфляцию, возможность разных процентных ставок по разным типам долга и т. д.

• [1] Маркс К., Энгельс Ф. Соч. 2-е изд. М.: Государственное издательство политической литературы, 1961. Т. 20. С. 131.
• [2] Капица С. П. Парадоксы роста. Законы развития человечества. С. 38−40.
• [3] Шабалин А. Н. Инвестиционное проектирование. М.: Московская финансово-промышленная академия, 2004. С. 47.