Модель ARMA. 
Эконометрика

Комбинация авторегрессионного процесса и процесса скользящей средней образует еще один класс временных моделей — ARMA (авторегрессия — скользящая средняя). Данная модель базируется на предположении о том, что текущее значения исследуемого временного ряда зависит только от линейной комбинации предыдущих значений временного ряда и белого шума. Модель ARMA (р, q) выглядит следующим образом:

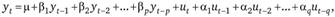(8.6).

где 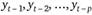и - значения лагов ряда и белых шумов соответственно.

Процесс ARMA можно записать при помощи оператора сдвига 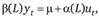где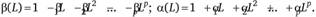

Процесс ARMA является комбинацией процессов AR и МА. Следовательно, свойства и характеристики процесса ARMA также являются комбинациями свойств и характеристик используемых процессов AR и МА.

Возникает вопрос: является ли процесс ARMA (р, q) стационарным? При условии нулевой средней процесс ARMA может быть представлен в виде при условии существования обратного оператора . При этом обратный оператор может быть разложен в сумму элементарных дробей, каждая из которых представима как бесконечно убывающая геометрическая прогрессия, т. е. в бесконечный операторный полином. При умножении на конечный полином снова получится бесконечный полином. Полученное выражение имеет смысл, только если корни характеристического уравнения ?(z) = 0 по модулю меньше единицы. Но в таком случае полученное выражение есть не что иное, как разложение Вольда, и, следовательно, процесс стационарен. Таким образом, процесс ARMA будет стационарен, только если стационарным будет используемый процесс AR. Аналогично, процесс ARMA будет обратимым, если существует обратный оператор 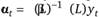. То есть процесс ARMA будет обратимым, если обратимым будет используемый процесс МА.

Найдем основные характеристики процесса ARMA. Очевидно, что математическое ожидание равняется нулю. Для того чтобы найти дисперсию процесса, представим процесс ARMA (р, q) в виде бесконечного процесса МА (?):

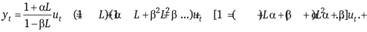
Тогда дисперсия у, равна.

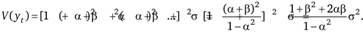
Автокорреляционные и частные автокорреляционные функции процессов AR, МА, ARMA обладают следующими свойствами.

• • Автокорреляционная функция авторегрессионного процесса убывает по экспоненте, а количество ненулевых лагов частной автокорреляционной функции равно порядку авторегрессионного процесса.
• • Частная авторегрессионная функция скользящей средней убывает по экспоненте, а число ненулевых лагов автокорреляционной функции равняется порядку процесса скользящей средней.
• • Авторегрессионная функция и частная авторегрессионная функция процесса авторегрессия — скользящая средняя убывает по экспоненте.

В табл. 8.2−8.12 приведены значения выборочных автокорреляционных и частных автокорреляционных функций стандартных процессов ARMA.

В табл. 8.2 представлена диаграмма автокорреляционных функций простейшего процесса скользящей средней. Как отмечалось выше, порядок скользящей средней может быть определен как число ненулевых лагов автокорреляционной функции. Существует значимая корреляция только с первым лагом. Следовательно, можно сделать вывод, что это скользящая средняя первого порядка.

Таблица 8.2. Выборочные автокорреляция и частная автокорреляция для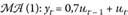

Autocorrelation	Partial Correlation	№	АС	РАС	Q-STAT	Prob
			0,481.	0,481.	61,667.	0,000.
			— 0,003.	— 0,305.	61,669.	0,000.
			— 0,043.	0,152.	62,159.	0,000.
			— 0,046.	— 0,135.	62,735.	0,000.
			— 0,036.	0,063.	63,087.	0,000.
			— 0,069.	— 0,127.	64,360.	0,000.
			— 0,074.	0,034.	65,845.	0,000.
			0,001.	0,015.	65,845.	0,000.
			0,070.	0,062.	67,202.	0,000.
			0,121.	0,074.	71,280.	0,000.
			0,061.	— 0,055.	72,236.	0,000.
			— 0,008.	0,026.	72,253.	0,000.

Таблица 8.3. Выборочные автокорреляция и частная автокорреляция для МA (1) с отрицательным коэффициентом: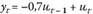

Autocorrelation	Partial Correlation	№	АС	РАС	Q-STAT	Prob
			— 0,443.	— 0,443.	52,110.	0,000.
			— 0,016.	— 0,264.	52,179.	0,000.
			— 0,009.	— 0,180.	52,199.	0,000.
			— 0,013.	— 0,143.	52,247.	0,000.
			0,024.	— 0,079.	52,399.	0,000.
			0,002.	— 0,041.	52,401.	0,000.
			— 0,067.	— 0,115.	53,628.	0,000.
			0,052.	— 0,058.	54,359.	0,000.
			— 0,043.	— 0,093.	54,862.	0,000.
			0,077.	0,011.	56,489.	0,000.
			0,013.	0,069.	56,533.	0,000.
			— 0,088.	— 0,034.	58,694.	0,000.

В табл. 8.3 также представлена диаграмма автокорреляционных функций скользящей средней первого порядка. Коэффициент при первом лаге процесса по модулю равен коэффициенту предыдущего процесса, но противоположен по знаку. Этот факт выражается в отрицательной корреляции первого лага автокорреляционной функции. Частная автокорреляционная функция, как должно бьггь у процесса скользящей средней, убывает по экспоненте.

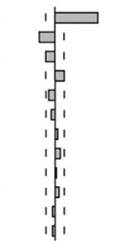
В табл. 8.4 представлены функции скользящей средней второго порядка. Как очевидно из диаграммы, значимая автокорреляция есть только с двумя первыми лагами. Более того, заметим, что поскольку оба коэффициента в модели положительны, корреляция с двумя первыми лагами также положительна.

Таблица 8.4. Выборочные автокорреляция и частная автокорреляция для

Autocorrelation	Partial Correlation	№	АС	РАС	Q-STAT	Prob
			0,602.	0,602.	96,296.	0,000.
			0,225.	— 0,215.	109,80.	0,000.
			— 0,040.	— 0,123.	110,23.	0,000.
			— 0,059.	0,119.	111,16.	0,000.
			— 0,068.	— 0,093.	112,42.	0,000.
			— 0,080.	— 0,055.	114,15.	0,000.
			— 0,073.	0,028.	115,59.	0,000.
			0,008.	0,076.	115,60.	0,000.
			0,079.	0,025.	117,30.	0,000.
			0,122.	0,049.	121,40.	0,000.
			0,080.	— 0,030.	123,18.	0,000.
			0,006.	— 0,045.	123,19.	0,000.

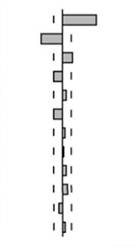
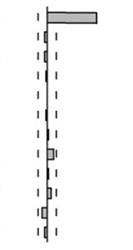
Таблица 8.5. Выборочные автокорреляция и частная автокорреляция для

Autocorrelation	Partial Correlation	№	АС	РАС	Q-STAT	Prob
			0,696.	0,696.	128,91.	0,000.
			0,462.	— 0,043.	186,00.	0,000.
			0,290.	— 0,031.	208,48.	0,000.
			0,173.	— 0,011.	216,52.	0,000.
			0,101.	0,001.	219,30.	0,000.
			0,049.	— 0,019.	219,93.	0,000.
			0,027.	0,015.	220,13.	0,000.
			0,063.	0,093.	221,22.	0,000.
			0,087.	0,017.	223,30.	0,000.
			0,114.	0,043.	226,88.	0,000.
			0,080.	— 0,069.	228,66.	0,000.
			0,032.	— 0,038.	228,94.	0,000.

В табл. 8.5 можем увидеть выборочные автокорреляции для простейшего авторегрессионного процесса первого порядка. Как уже отмечалось, порядок авторегрессионной функции может быть найден по количеству ненулевых лагов частной автокорреляционной функции. В данном модельном примере это наглядно видно. Значимая корреляция есть только с первым лагом. При этом автокорреляционная функция, как и говорилось ранее, убывает по экспоненте.

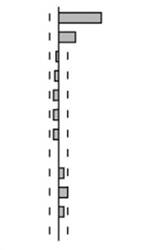
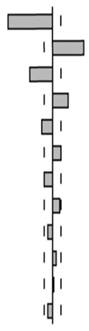
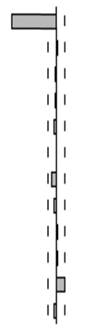
В табл. 8.6 представлены диаграммы функций для авторегрессионного процесса первого порядка с отрицательным коэффициентом. Отрицательность коэффициента наглядно отражается в отрицательной значимой корреляции с первым лагом.

Таблица 8.6. Выборочные автокорреляция и частная автокорреляция для AR (1) с отрицательным коэффициентом: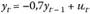

Autocorrelation	Partial Correlation	№	АС	РАС	Q-STAT	Prob
			— 0,676.	— 0,676.	121,51.	0,000.
			0,469.	0,023.	180,33.	0,000.
			— 0,337.	— 0,022.	210,80.	0,000.
			0,229.	— 0,022.	224,96.	0,000.
			— 0,172.	— 0,028.	232,95.	0,000.
			0,129.	0,003.	237,48.	0,000.
			— 0,133.	— 0,069.	242,28.	0,000.
			0,102.	— 0,034.	245,12.	0,000.
			— 0,067.	0,020.	246,34.	0,000.
			0,057.	0,020.	247,24.	0,000.
			0,025.	0,128.	247,41.	0,000.
			— 0,079.	— 0,043.	249,16.	0,000.

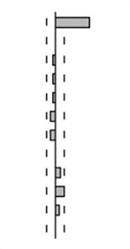
Таблица 8.7. Выборочные автокорреляция и частная автокорреляция для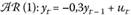

Autocorrelation	Partial Correlation	№	AC	РАС	Q-STAT	Prob
			0,321.	0,321.	27,495.	0,000.
			0,082.	— 0,024.	29,301.	0,000.
			— 0,009.	— 0,032.	29,324.	0,000.
			— 0,037.	— 0,026.	29,700.	0,000.
			— 0,032.	— 0,011.	29,984.	0,000.
			— 0,056.	— 0,046.	30,839.	0,000.
			— 0,071.	— 0,044.	32,204.	0,000.
			0,016.	0,060.	32,273.	0,000.
			0,047.	0,028.	32,877.	0,000.
			0,111.	0,089.	36,292.	0,000.
			0,054.	— 0,015.	37,110.	0,000.
			— 0,018.	— 0,043.	37,204.	0,000.

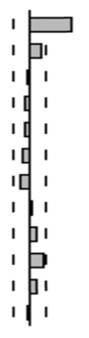
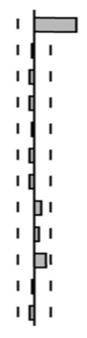
В табл. 8.7 представлены автокорреляционные диаграммы авторегрессионной модели первого порядка с коэффициентом 0,3. Порядок модели наглядно можно определить из частной автокорреляционной функции. Заметим, что если сравнить коррелограмму этой модели с коррелограммой модели, представленной на таблице 8.5, то можно увидеть, что меньшее по модулю значение коэффициента отразилось в меньшей корреляции частной автокорреляционной функции с первым лагом.

В табл. 8.8 представлены диаграммы выборочных функций корреляций авторегрессионного процесса второго уровня. Оба коэффициента в модели положительны, поэтому существует значимая положительная корреляция с двумя первыми лагами. Заметам, что автокорреляционная функция не убывает по экспоненте. Этот факт наталкивает на мысль о нестационарности ряда.

Таблица 8.8. Выборочные автокорреляция и частная автокорреляция для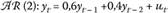

Autocorrelation	Partial Correlation	№	АС	РАС	Q-STAT	Prob
			0,945.	0,945.	237,47.	0,000
			0,931.	0,358.	468,98.	0,000
			0,900.	— 0,033.	686,06.	0,000
			0,877.	— 0,007.	892,85.	0,000
			0,853.	0,025.	1089,6.	0,000
			0,832.	0,013.	1277,2.	0,000
			0,808.	— 0,017.	1455,2.	0,000
			0,794.	0,070.	1627,4.	0,000.
			0,772.	— 0,016.	1791,0.	0,000.
			0,755.	— 0,012.	1947,9.	0,000.
			0,729.	— 0,071.	2094,9.	0,000.
			0,702.	— 0,086.	2231,7.	0,000.

Таблица 8.9. Выборочные автокорреляция и частная автокорреляция для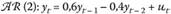

Autocorrelation	Partial Correlation	№	АС	РАС	Q-STAT	Prob
			0,441.	0,441.	51,829.	0,000.
			— 0,144.	— 0,420.	57,345.	0,000.
			— 0,277.	— 0,002.	77,927.	0,000.
			— 0,117.	— 0,004.	81,589.	0,000.
			0,021.	— 0,031.	81,712.	0,000.
			— 0,003.	— 0,080.	81,715.	0,000.
			— 0,068.	— 0,039.	82,974.	0,000.
			— 0,024.	0,039.	83,126.	0,000.
			0,062.	0,018.	84,184.	0,000.
			0,129.	0,085.	88,772.	0,000.
			0,075.	— 0,017.	90,317.	0,000.
			— 0,009.	0,026.	90,340.	0,000.

В табл. 8.9 можно увидеть диаграммы функций для авторегрессионного процесса второго порядка. Коэффициенты в модели имеют разные знаки, что отражается в разных знаках значимой корреляции первых двух лагов частной автокорреляционной функции. Кроме того, модуль автокорреляционной функции, как было описано в теории, убывает по экспоненте.

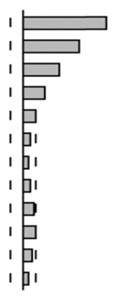
В табл. 8.10 представлены данные стандартного процесса ARMA (1, 1). Автокорреляционная функция и модуль значений частной автокорреляционной функции процесса убывает по экспоненте. Заметим, что к 12-му лагу обе корреляционные функции убывают почти до нулевого уровня.

Таблица 8.10. Выборочные автокорреляция и частная автокорреляция для

Autocorrelation	Partial Correlation	№	АС	РАС	Q-STAT	Prob
			0,835.	0,835.	185,55.	0,000.
			0,559.	— 0,458.	268,96.	0,000.
			0,356.	0,241.	302,87.	0,000.
			0,216.	— 0,166.	315,46.	0,000.
			0,125.	0,098.	319,69.	0,000.
			0,066.	— 0,076.	320,89.	0,000.
			0,048.	0,128.	321,52.	0,000.
			0,070.	0,019.	322,85.	0,000.
			0,101.	0,031.	325,67.	0,000.
			0,115.	— 0,020.	329,30.	0,000.
			0,088.	— 0,085.	331,47.	0,000.
			0,046.	0,043.	332,05.	0,000.

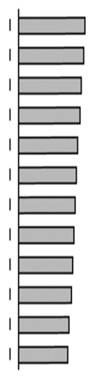
Таблица 8.11. Выборочные автокорреляция и частная автокорреляция для процесса случайного блуждания: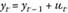

Autocorrelation	Partial Correlation	№	AC	РАС	Q-STAT	Prob
			0,975.	0,975.	252,65.	0,000
			0,948.	— 0,025.	492,88.	0,000
			0,922.	— 0,030.	720,55.	0,000
			0,896.	0,019.	936,73.	0,000
			0,873.	0,027.	1142,7.	0,000
			0,850.	— 0,009.	1338,7.	0,000
			0,828.	0,007.	1525,4.	0,000
			0,810.	0,064.	1704,7.	0,000.
			0,790.	— 0,048.	1876,0.	0,000.
			0,770.	— 0,018.	2039,1.	0,000.
			0,745.	— 0,091.	2192,6.	0,000.
			0,719.	— 0,041.	2335,9.	0,000.

В табл. 8.11 представлены выборочные автокорреляционная и частная автокорреляционная функции процесса случайного блуждания. Модель случайного блуждания — классический пример нестационарного ряда. Как можно увидеть, нестационарность ряда отражается в очень медленном убывании автокорреляционной функции. Интересно заметить, что, по сути, процесс случайного блуждания является авторегрессионным процессом с единичным коэффициентом. Частная автокорреляционная функция и в этом примере хорошо определяет порядок авторегрессионной функции.

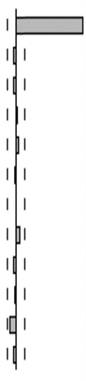
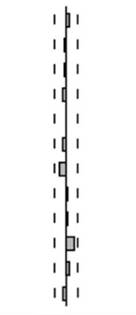
В табл. 8.12 представлены корреляционные данные модельного примера белого шума. Ни у автокорреляционной функции, ни у частной автокорреляционной функции не наблюдается значимой корреляции ни с одним из лагов.

Таблица 8.12. Выборочные автокорреляция и частная автокорреляция для процесса белого шума: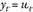

Autocorrelation	Partial Correlation	№	АС	РАС	Q-STAT	Prob
			0,026.	0,026.	0,1880.	0,000.
			— 0,011.	— 0,012.	0,2203.	0,000.
			— 0,021.	— 0,020.	0,3362.	0,000.
			— 0,030.	— 0,029.	0,5748.	0,000.
			— 0,008.	— 0,007.	0,5917.	0,000.
			— 0,033.	— 0,034.	0,8972.	0,000.
			— 0,072.	— 0,072.	2,3182.	0,000.
			0,024.	0,026.	2,4761.	0,000.
			0,016.	0,012.	2,5497.	0,000.
			0,095.	0,091.	5,0685.	0,000.
			0,040.	0,033.	5,5093.	0,000.
			— 0,048.	— 0,048.	6,1559.	0,000.

Чтобы ответить на вопрос, является ли ряд стационарным, можно воспользоваться тестом Дики - Фуллера.

Стандартный тест Дики — Фуллера заключается в проверке гипотезы стационарности временного ряда.

В рамках теста рассматривается модель.

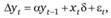(8.7).

где а = р Т.

Нулевая и альтернативная гипотеза записываются в следующем виде:

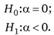
Оценка происходит на базе статистики Стьюдента 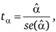где  — оценка а; 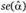 — стандартное отклонение.

В 1979 г. Д. Дики и У. Фуллер [Dickey, Fuller] показали, что при условии наличии единичного корня рассматриваемая статистика не подчиняется распределению Стьюдента. Оказалось, что простой тест Дики — Фуллера применим только для моделей AR (1).

В расширенном тесте Дики - Фуллера (ADF) учитывается корреляция лагов высших порядков путем предположения о том, что у, описывается моделью AR (р) и добавлением разностей порядка р в правую часть уравнений.

(8.8).

Фуллер доказал, что асимптотическое распределение ?-статистики для, а не зависит от количества лагов разностей, включенных в ADF-тест. Более того, в 1984 г. Дики доказал, что еслиу, описывается моделью AR (р), то ADF-тест асимптотически эффективен при присутствии МА компонент.