Собственные колебания системы с бесконечным числом степеней свободы

Система с непрерывно распределенной массой имеет бесконечно большое число степеней свободы, поэтому и метод решения задачи о колебаниях такой системы будет другой. Для того чтобы получить некоторое представление об особенности решения такой задачи, рассмотрим собственные колебания простой балки (рис. 15.30, а).

При отклонении балки от первоначального состояния возникают силы инерции, интенсивность которых в произвольной точке с координатой х будет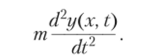

Дифференциальное уравнение равновесия элемента балки в любой момент времени t запишется в частных производных:

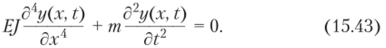
Здесь т — масса единицы длины балки.

Теперь будем искать решение дифференциального уравнения в виде.

где X — функция от х; Т — функция от времени t. Подставляя выражение (15.44) в уравнение (15.43), получим.

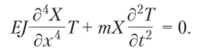
После несложных преобразований приведем это уравнение к виду.

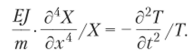
В левой части этого равенства как в числителе, так и в знаменателе содержатся функции, зависящие только от х, а в правой — только от t. Такое равенство возможно в том случае, когда частное от деления числителя на знаменатель в обоих случаях есть величина постоянная:

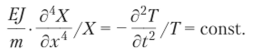
Обозначим эту константу со². Приравнивая этой величине каждую из величин предыдущего равенства, получим два дифференциальных уравнения уже в обыкновенных производных:

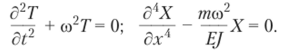
Решение первого уравнения нам уже известно:

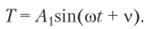
Решение второго уравнения четвертого порядка состоит из четырех слагаемых.

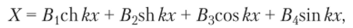
ТП (о^2.

^ГДС*'Гw

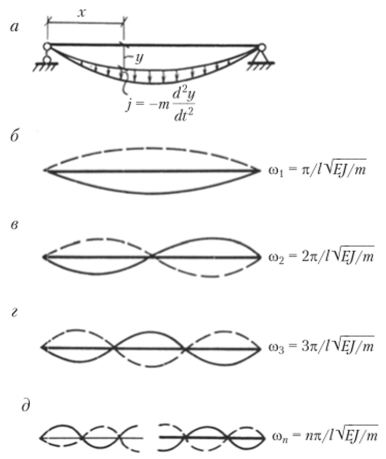
Рис. 1530.

Постоянные В> В₂, В% и В_А зависят от граничных условий. Для балки на двух опорах (см. рис. 15.30, а) должны быть удовлетворены следующие граничные условия: при х = 0 и при х = / прогибы равны нулю. Этому условию удовлетворяет только последнее слагаемое.

Итак, X = В₄sin kx.

Из условия у{1) = 0 находим sin kl = 0kl = л, 2л,…, юг. Учитывая выражение для к, получим.

Окончательно из условия (15.44) имеем.

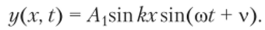
Формы колебаний определяются функцией от х> а именно синусоидой sinkx. При различных к они показаны на рис. 15.30, б — д.