Другие определении системы действительных чисел

Определении системы действительных чисел с помощью понитий сечении и верхней границы Впервые теория действительных чисел была построена выдающимся немецким математиком Р. Дедекиндом. Она основана на понятии сечения.

5.7.1. Определение. Пусть дано линейно упорядоченное множество ,. Упорядоченная пара подмножеств (А, В) из Р, называется сечением, если выполняются следующие условия: 1).

Л*0, Вф0 2) АглВ = 0; 3) AJВ = Р 4) для любых аеА,.

be В выполняется неравенство а <�Ь.

5.7.2. Определение. Пусть (А, В) — сечение линейно упорядоченного множества. Наибольший элемент в А и наименьший элемент в В (если они существуют) называются.

граничными элементами сечения.

Нетрудно понять, что всякое сечение может иметь не более двух граничных элементов. Покажем, что все три оставшиеся возможности реализуются.

Пример сечения с двумя граничными элементами. Рассмотрим линейно упорядоченное множество натуральных чисел (jV, <) и в нем подмножества А = {а е N а < 3} и В = {b е N b > 3}. Понятно, что {А, В) — сечение и числа 3 и 4 являются его граничными элементами.

Пример сечения с одним граничным элементом. Рассмотрим линейно упорядоченное множество действительных чисел (/?,<) ив нем подмножества А = {а е R, а < л/З} и В = {b е R> . Ясно, что.

{А, В) — сечение и единственным его граничным элементом является л/З — наибольшее число в А.

Пример сечения, не имеющего граничных элементов. Рассмотрим линейно упорядоченное множество рациональных чисел (Q, <) и в нем подмножества A- {a eQa и В = {b eQ> yfb}. Понятно, что (А, В) — сечение. Поскольку v3 не является рациональным числом, го граничного элемента нет.

Определение системы действительных чисел по Дедекинду формулируется следующим образом.

5.7.3. Определение. Системой действительных чисел называется упорядоченное поле, в котором выполняется аксиома Дедекинда: всякое сечение упорядоченного поля имеет граничный элемент.

Вспомним, что геометрическим представлением множества действительных чисел является числовая прямая. Понятно, что если из прямой удалить некоторую точку, то она перестает быть непрерывной, оставшееся множество точек уже нельзя начертить, не прерываясь. В то же время, образовавшийся пробел разделяет прямую на два подмножества точек А и /?, причем пара (А, В) образует сечение оставшегося множества точек. Это сечение не имеет граничного элемента, так как ни в А нет наибольшего элемента, ни в В нет наименьшего. Требование выполнимости аксиомы Дедекинда заставляет нас вернуть на прямую удаленную точку и тем самым восстановить сс непрерывность. Таким образом, аксиома Дедекинда, сформулированная для точек прямой, наглядно выражает ее непрерывность.

Не менее наглядное выражение свойства непрерывности прямой, а вместе с тем и системы действительных чисел, дает аксиома о точной верхней границе. Дадим определение соответствующих понятий. Напомним, что понятия верхней и нижней границ данного множества даны в 2.4.15.

• 5.7.4. Определение. Пусть А — непустое подмножество линейно упорядоченного множества (Р, <). Верхняя 1раница с множества А называется точной верхней границей этого множества, если для любой верхней границы b выполняется неравенство с<�Ь. Точная верхняя граница множества А обозначается sup, 4 (читается: супремум А).
• 5.7.5. Определение. Системой действительных чисел называется упорядоченное поле (/?,+,-,<), в котором выполняется аксиома о точной верхней границе: всякое непустое ограниченное сверху; подмножество из R имеет в R точную верхнюю границу.

Установим эквивалентность определений системы действительных чисел 5.1.4,5.73 и 5.7.5 по следующей схеме: 5.1.4 => 5.7.3 => 5.7.5 => 5.1.4.

5.7.6. Теорема. Если в упорядоченном поле выполняются аксиома Архимеда и аксиома Кантора, то выполняется и аксиома Дедекинда.

Доказательство. Пусть в упорядоченном поле (Р, +, •, <) выполняются аксиома Архимеда и аксиома Кантора и пусть (А, В) — сечение в Р. Поскольку А*0 и Р * 0, то существуют а₀ е А, Ь₍₎е В.

Разделим отрезок [а₀, Ь₀] пополам точкой ^а° и через [а_{, Ь]

обозначим ту из половин отрезка [а₀, Ь₀], для которой а_хеА, />, е В. Отрезок разделим пополам и через [а₂, Ь₂] обозначим ту половину, для которой а₂еА, fyeB, итак далее. В результате получим последовательность вложенных отрезков ([я_м, 6"]), для которой, по аксиоме Кантора, существует элемент с е Р, принадлежащий всем отрезкам последовательности. По определению сечения, либо се Л, либо с е В.

Пусть се, А у докажем, что с является наибольшим элементом в А. Предположим противное: пусть существует элемент а е А такой, что с<�а. Тогда для любого neN имеем: а_п<�с<�а<�Ь_п, откуда О <�а-с<�Ь"-а" = и 2^п (а — с) < Ь₀ — а₀, что противоречит аксиоме Архимеда. Следовательно, а <�с для любого а то есть с — наибольший элемент в А.

Если предположить, что се В, то аналогично можно доказать, что с является наименьшим элементом в В. Итак, с — граничный элемент сечения (А, В). ?

5.7.7. Теорема. Если в упорядоченном поле выполняется аксиома Дедекинда, то выполняется и аксиома о точной верхней границе.

Доказательство. Пусть в упорядоченном поле (Р, +, •, выполняется аксиома Дедекинда и пусть М — непустое подмножество в Р, ограниченное сверху некоторым элементом с е Р. Если в М есть наибольший элемент, то он и является точной верхней границей этого подмножества. Предположим, что в М нет наибольшего элемента. Рассмотрим подмножества (рис. 13): А = {а е Р существует .v е М такой, что а < х}, В = {b е Р х < b для любого хеМ).

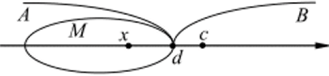
Рис. /3

Следуя определению 5.7.1, докажем, что пара подмножеств (А, В) является сечением. Множество А содержит непустое подмножество М, значит А * 0.

Так как элемент с, по условию, является верхней границей множества М и, по предположению, в М нет наибольшего элемента, то для любого х е М имеем: х<�с. Следовательно, с е В и В Ф 0.

Непосредственно из определения подмножеств А и В вытекает, что АсВ = 0 и AkjB = Р.

Пусть аеА, be В. Тогда, по определению подмножеств A w В, существует хеМ такой, что а<�х<�Ь, откуда а .

Итак, {А, В) — сечение, и, по аксиоме Дедекинда, существует граничный элемент этого сечения, который обозначим через d. Предположим, что d е А. Тогда существует хеМ такой, что d <�х.С другой стороны, так как d — наибольший элемент в А и М с И, то х < d. Таким образом d = х е М и является там наибольшим элементом, что Следовательно, d еВ. Очевидно, всякая верхняя граница множества М принадлежит В, а так как d — наименьший элемент в В, то d = supM. ?

5.7.8. Теорема. Если в упорядоченном поле выполняется аксиома о точной верхней границе, то выполняются также аксиома Архимеда и аксиома Кантора.

Доказательство. Пусть в упорядоченном поле (Р, +, •, выполняется аксиома о точной верхней границе. Установим сначала выполнимость аксиомы Архимеда. Пусть а, ЬеР и а>0. Докажем существование натурального числа п такого, что па>Ь. Предположим противное, пусть па<�Ь для любого neN. Тогда множество М = {па | neN} не пусто и ограничено сверху элементом Ь. По условию, существует с = supМ. Так как 0, то с-а и с—а уже не является верхней границей множества М. Следовательно, существует натуральное число к такое, что ка>с-а. Отсюда (к +1 )а > с — пришли к противоречию, ибо с есть верхняя граница множества М. Таким образом, существует натуральное число п такое, что па>Ь.

Докажем теперь выполнимость аксиомы Кантора. Пусть дана последовательность вложенных отрезков (["",?"])• Множество А = {а_п | п е N) не пусто, и всякий элемент Ь_п является его верхней границей. По условию, существует supAf = d. Но тогда d принадлежит всем отрезкам данной последовательности. ?

5.7.9. Определение. Последовательность элементов (х").

упорядоченного поля (Р, +, •, <) называется фундаментальной, если для любого положительного ? € Р существует номер к такой, что для всех г > к ₉ s> к выполняется неравенство | x_r -x_s | < е.

Напомним, что если в упорядоченном поле lim х_п =я, то говорят,.

п—>00.

что последовательность (х") сходится (к элементу а).

5.7.10. Теорема. Если упорядоченное поле удовлетворяет аксиоме Архимеда, то оно удовлетворяет аксиоме Кантора тогда и только тогда, когда всякая его фундаментальная последовательность сходится.

Доказательство. (=>) Докажем, что в упорядоченном поле действительных чисел (в смысле определения 5.1.4) произвольная фундаментальная последовательность (х_п) сходится.

Сначала установим существование отрезка, содержащего все члены последовательности. По определению фундаментальной последовательности, для числа ?>0 существует номер г такой, что для любого s > г выполняется неравенство | x_s -x_r < 1, откуда | | = | (.Ту — Х_г) + Х_г | ^ | ЛГу ^— ЛГ_Г | + | Х_г | С 1+ | Х_;. |.

Если/и = тах{|х₀|,…,|х_г|, 1+|х_г |}, то |х_я|</и для любого п, то есть —т<�х_п<�т. Обозначив а₀ = -т, Ь₀=т, получим, что все члены данной последовательности принадлежат отрезку [д₀, 6₀]? Положим Xj =х₀. Разделим озрезок [а^Ь^] пополам и через [я^].

обозначим ту его половину, которая содержит бесконечное множество элементов данной последовательности, а через х_/( обозначим произвольный член последовательности (х_п), принадлежащий отрезку [Я|,^]. Отрезок [a_hdj] снова разделим пополам и аналогично выберем половину [я₂,^] и член последовательности х^, содержащийся в ней.

В результате получим последовательность вложенных отрезков ([а", Ь"]) и подпоследовательность (х,) данной последовательности (х_л). По аксиоме Кантора, существует число с, принадлежащее всем отрезкам последовательности ([а", Ь"]). Докажем, что lim х_п — с.

п-*х>

Пусть е — произвольное положительное действительное число. Из аксиомы Архимеда следует существование натурального числа т

такого, что Ь₀-а₀< 2'^м-|?, откуда Ь_т ~а_т = ——— <^. Очевидно, для всех п>т имеем: х, е[а_п9Ь_пс[а_т9Ь_т], откуда последовательности вытекает, что для — существует номер к такой,.

?

что для всех п>к, i_n >к выполняется неравенство l*,-*, |< —. Пусть / = max {?,///}. Тогда для всех n>t имеем:

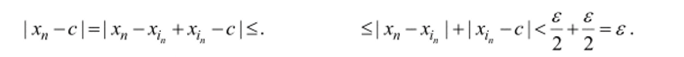
Следовательно, lim х_п = с.

п—*х>

(<=) Предположим теперь, что в упорядоченном поле (Р,+,-,<) выполняется аксиома Архимеда и всякая фундаментальная последовательность сходится. Рассмотрим последовательность ([в", Ь_п]) вложенных отрезков из Р и докажем существование в Р элемента, принадлежащего всем отрезкам этой последовательности. Обозначим а₀ =.т₀, Ь₀=у₀ и разделим отрезок [;с₀,^₀] пополам. Если середина.

*о⁺То отрезка ^и ^ ^u принадлежит всем отрезкам данной последовательности, то утверждение доказано. Пусть существует отрезок данной последовательности, не содержащий^. Тогда он содержится в одной из половин отрезка [jc₀, j₀], которую обозначим через [*|,.У|]. Разделим этот отрезок снова пополам и повторим рассуждения. В результате либо на некотором шаге мы обнаружим элемент, который принадлежит всем огрезкам данной последовательности, либо построим последовательность вложенных отрезков [х_п, у_п], каждый из которых содержит некоторый отрезок данной последовательности ([а_п,/>"]).

Предположим, что имеет место второй случай. Обозначим ^z2n ^=хп" ^z2n+i =У_пл = 0,1,… Легко доказать, что последовательность.

(z_n) является фундаментальной. По условию, существует lim z_n = с;

п—>5С очевидно, с принадлежит всем отрезкам последовательности ([*",>>"]). Докажем, что с принадлежит всем отрезкам данной последовательности (["",/>"]). Предположим противное: пусть существует номер к такой, что сё[а_к, Ь_к]. Тогда либо с<�а_к<�Ь_к, либо а_к<�Ь_к<�с. Рассмотрим первый случай (во втором случае рассуждения аналогичны). Так как limz"=c, то.

просуществует номер m такой, что у_m -с < а_к -с, откуда у,"<�а_к. Но тогда отрезки [х_т, у_т] и [х_к, у_к] не имеют общих элементов, а значит отрезок [х_т, у_т] не содержит ни одного отрезка данной последовательности ([я",/?"]), что противоречит предположению.? Доказанная теорема показывает, что систему действительных чисел можно определить следующим образом.

5.7.11. Определение. Системой действительных чисел называется упорядоченное поле, в котором выполняется аксиома Архимеда и всякая фундаментальная последовательность сходится.

Упражнения

• 1. Всякое ли сечение линейно упорядоченного множества натуральных чисел имеет два 1раничных элемента?
• 2. Опишите виды сечений линейно упорядоченного множества рациональных чисел.
• 3. На примерах покажите разницу между понятиями наибольшего элемента данного множества, его верхней границы и точной верхней границы.
• 4. Приведите пример линейно упорядоченного множества (упорядоченного поля), в котором не выполняегся аксиома о точной верхней 1ранице.
• 5. Приведите пример фундаментальной последовательности в упорядоченном поле рациональных чисел, которая не являлась бы в нем сходящейся.
• 6. Приведите примеры различных фундаментальных последовательностей рациональных чисел, сходящихся к одному и тому же действительному числу.
• 7. Из доказательства теоремы 5.7.11 извлеките доказательство того, что,

если в упорядоченном поле выполняется аксиома Архимеда, то в нем всякая фундаментальная последовательность содержит сходящуюся подпоследовательность.