Принципы формирования страховых резервов

Перейдем непосредственно к формированию актуарного резерва — основного вида резервов в долгосрочном страховании жизни. Рассмотрим пример. Страхователь в возрасте х заключает договор страхования на дожитие сроком на п лет. Взнос единовременный. Нетто-ставку обозначим Р₀ и определим как Р₀ = _пЕ_х.

Теперь представим, что ровно через год приходит тот же самый страхователь и хочет заключить еще один договор так, чтобы он заканчивал свое действие одновременно с первым. Возраст страхователя для нового договора уже не х, а х + 1. Срок страхования не п лет, а п — 1. Нетто-ставку обозначим Р_а и она составит Р_г = _п__гЕ_{х + v} Очевидно, что при увеличении возраста и сокращении срока страхования страхователю необходимо уплатить больший взнос, поэтому Р, > Р₀.

Пусть проходит еще один год, и страхователь является за новым договором с условием, что он должен завершаться одновременно с предыдущими двумя. Нетрудно догадаться, что нетто-ставка Р₂ = «_ ₂Е_Х + ₂ и Р₂ > Р].

Представим это на схеме (рис. 2.3).

Далее можно продолжать до момента окончания всех договоров страхования. Получаем последовательность нетто-ставок в каждый момент времени t между моментами Оип — началом и окончанием первого договора страхования. Данную последовательность можно представить в виде рис. 2.4.

Мы помним, что нетто-ставка (нетто-взнос, если применяется страховая сумма) отражает сумму средств, которые необходимо получить от страхователя при заключении договора страхования, чтобы впоследствии иметь возможность исполнять перед ним финансовые обязательства, а именно ожидаемую современную стоимость будущих выплат. Исходя из этого принципа, каждый год мы рассчитываем страхователю по каждому из его договоров _пЕ_х, «_ Е_Х + _{ь п}_₂Е_Х + 2> Собрав указанные нетто-ставки в единую последовательность и разместив на единой оси времени, мы видим, что элементы последовательности отражают размер средств в каждом страховом году, необходимый для осуществления будущей выплаты по дожитию. Вспоминая определение страховых резервов и пояснения к нему, приходим к выводу, что наша последовательность не что иное, как математический резерв.

Рис. 2.3. Три договора страхования на дожитие для страхователя в возрасте х, х + 1 и х + 2, со сроками страхования п, п — 1, л — 2 соответственно.

ные. 2.4. Последовательность нетто-ставок для договоров страхования на дожитие. Возраст страхователя х е [х, х + л]. Срок страхования п е [0, л].

Для численной иллюстрации примера на рисунке представлен расчет величин _пЕ_х, _п_ ₁Е_{Х + г}, _п_ ₂Е_Х + ₂, … (т. е. изменение математического резерва в зависимости от года страхования) для застрахованного в возрасте 35 лет, договора страхования сроком на 10 лет и страховой суммы 100 000 руб.

Из представленных логических выкладок, формул и рис. 2.5 можно сделать важный вывод: для договоров с единовременной уплатой взноса математический резерв в момент 0 в точности равен нетто-взносу, а в момент п математический резерв в точности равен страховой сумме.

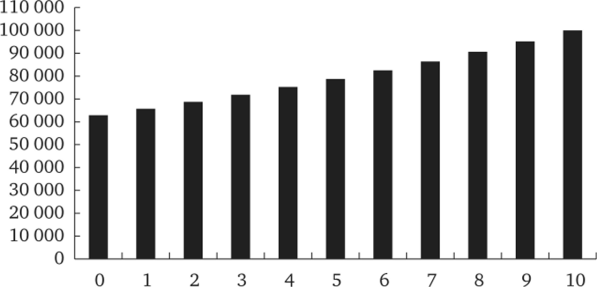
Рис. 2.5. Изменение математического резерва в зависимости от года страхования для договора с единовременным взносом.

Рассмотрим пример для случая уплаты взносов в рассрочку. Применим тот же самый принцип, что и для договора с единовременным взносом. Застрахованный в возрасте х заключает договор страхования на срок п лет, затем последовательно заключает еще несколько договоров с интервалом в один год. Все договоры заканчиваются в одну и ту же дату.

?

Итак, в первый год страхования имеем нетто-ставку Р₀ - ^п_ ^х ,.

а ~

х:п I.

и очевидно, что _пЕ_х-Р₀ а -г = 0. Ставку по договору № 2 обозна;

чим Рj. Рассчитываться она будет как Р_а = «~^г *⁺¹, и при этом.

^ал-₊1:^Й1.

Pj > Р₀ ввиду того, что срок договора страхования сокращается на один год по сравнению с договором № 1 и застрахованный становится на год старше.

Теперь рассмотрим выражение _п__г Е_х+1 — Р₀ й_А.₊₁,—j-j. Эта разность будет больше нуля, так как _п-Е_х+1>_пЕ_х (см. пример для единовременного взноса), < й_х.^ (дисконтирование взносов на один год меньше, следовательно, в ^ на одно слагаемое меньше, чем в й^), а _пЕ_х-Р₀а_х, —1=0. Таким образом, если бы страховщик решил для договора № 2 использовать взнос Р₀ из договора № 1, то у него при заключении договора № 2 уже заранее должны быть накоплены некоторые средства, чтобы впоследствии обеспечить будущие выплаты застрахованному. Если использовать взнос Р₀ и не иметь созданных заранее накоплений, то баланс обязательств страховщика и страхователя будет нарушен.

Разница _n_, E_x+t-P₀a -^ будет увеличиваться с каждым страховым годом f и составит последовательность значений, экономический смысл которых уже описан выше — это средства, необходимые страховщику в каждый момент времени для исполнения своих обязательств, математический резерв. На рис. 2.6 показано постепенное изменение математического резерва для договора страхования с уплатой взносов раз в год, срок страхования 10 лет, страховая сумма 100 000 руб., застрахованный в возрасте 35 лет.

Рис. 2.6. Изменение математического резерва в зависимости от года страхования для договора с рассроченными взносами.

По аналогии с договором страхования с единовременным взносом делаем выводы относительно величины резерва на момент начала и окончания договора страхования:

• • на момент 0 математический резерв равен точно 0;
• • на момент п математический резерв равен точно страховой сумме.

Далее будут отдельно описаны случаи, когда указанные закономерности не выполняются.

В актуарной литературе математический резерв имеет специальное обозначение _tV. Формулы для наиболее распространенных типов страховых покрытий имеют следующий вид:

• страхование на дожитие:

_tV =_n-t^x+t Д^ля единовременного взноса, tV=n-tE_x+t-Pa_x+t—i для годовых взносов;

• страхование жизни на срок (на случай смерти):

= ^ для единовременного взноса,.

,^v = — Pa_x+t—_} для годовых взносов;

• смешанное страхование жизни (страховые суммы по дожитию и по случаям смерти одинаковы):

_t V = A_x+r^| для единовременного взноса,.

tV = A_x+t:n^ -Pa_x+t—i для годовых взносов.

В качестве примера сделаем расчет математического резерва для смешанного страхования жизни и страхования жизни на срок. Застрахованный: мужчина, 35 лет, срок страхования 15 лет. Страховая сумма 1 000 000 руб. РФ. Норма доходности 4% годовых. Расчет для смешанного страхования жизни представлен в табл. 2.1, для страхования жизни на срок — в табл. 2.2.

На рис. 2.7 математический резерв представлен графически.

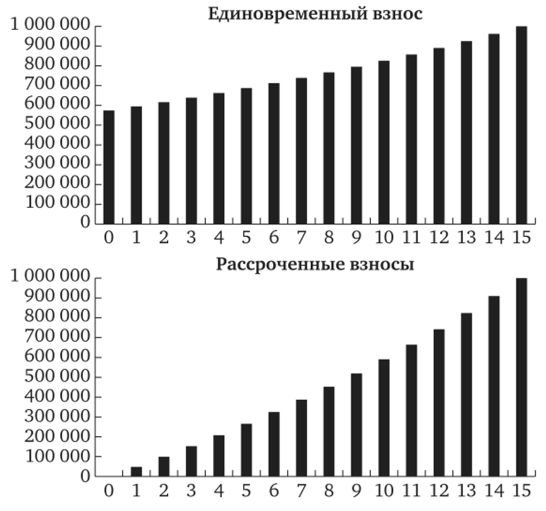
Рис. 2.7. Математический резерв для смешанного страхования.

жизни Расчет математического резерва для смешанного страхования жизни.

Расчет математического резерва для страхования жизни на срок.

Для наглядности на рис. 2.8 дано графическое представление математического резерва для страхования жизни на срок.

Рис. 2.8. Математический резерв для страхования жизни на срок.

На основе полученных расчетов и графических представлений резервов можно сделать следующие наблюдения:

• • для смешанного страхования жизни:
  • — при единовременном взносе резерв начинается из неттовзноса, постепенно растет и к концу срока страхования становится равным страховой сумме,
  • — при рассроченных взносах резерв начинается из нуля, постепенно растет и к концу срока страхования становится равным страховой сумме;
• • для страхования жизни на срок:
• — при единовременном взносе резерв начинается из неттовзноса, постепенно снижается и к концу срока страхования становится равным нулю,
• — при рассроченных взносах резерв начинается из нуля, постепенно растет, затем постепенно снижается и к концу срока страхования становится равным нулю.

Поведение математического резерва для обеих программ закономерно. Смешанное страхование жизни относится к накопительным программам. Оно предусматривает дожитие застрахованного до конца срока страхования и крупную выплату по окончании договора. Поэтому резерв всегда большой, возрастает и должен достигать размера страховой суммы. Ранее такой сценарий развития математического резерва мы видели на примере страхования на дожитие. Описанное поведение резерва характерно для всех программ страхования, предусматривающих дожитие застрахованного лица до конца срока страхования.

Страхование жизни на срок не содержит в своей структуре риск «Дожитие» и относится к рисковым программам. Здесь нет необходимости держать резервы большого размера, так как страхуется только риск смерти. Если застрахованное лицо доживает до конца срока договора, то никакой выплаты не производится, поэтому резерв становится равным нулю. При этом в договоре с единовременным взносом резерв постепенно амортизируется до нуля, а договоре с рассроченным взносом резерв сначала накапливается (поступают взносы), потом с истечением договора также амортизируется до нуля.

По другим видам страховых покрытий, не рассмотренным в данном параграфе, получить формулы для расчета математического резерва предлагается самостоятельно на основе нижеследующего примера, демонстрирующего подходы к выводу формул.