Особенности нейросетевого моделирования обратной коэффициентной задачи

Аннотация: В работе исследуются возможности применения нейронных сетей к задачам обратного расчета многослойной дорожной конструкции. Рассматриваются сети с различной архитектурой. Для улучшения условий сходимости применяются процедура обратного распространения с автоматическим выбором шага, разные виды активационных функций с варьируемыми параметрами.

Ключевые слова: нейронные сети, обратные задачи, полутораслойный предиктор, двухслойный перцептрон, аппроксимация, активационные функции.

нейронный сеть многослойный варьируемый Использование нейронных сетей дает качественно новый подход к решению задач прогнозирования поведения дорожной конструкции при изменении исходных данных, в частности, свойств используемых материалов. Данная работа является продолжением начатого ранее исследования [1], посвященного нейросетевому моделированию обратной коэффициентной задачи. В дополнение работы [1] для улучшения условий сходимости в процедуре обратного распространения увеличено число варьируемых параметров, использована процедура автоматического выбора шага, также проведен сравнительный анализ сетей с различной архитектурой.

Решению обратной задачи предшествовало создание нейросетевой модели рассматриваемой многослойной конструкции. Решение прямой задачи сводилось к задаче многомерной аппроксимации. Как известно [2], нейронные сети способны аппроксимировать с любой точностью любую непрерывную функцию многих переменных.

Одна и та же многомерная функция может моделироваться сетями различной архитектуры [3−8], что существенно влияет на объем вычислений и получаемую точность результатов. В рассматриваемой задаче условия нагружения таковы, что зависимость характеристик деформирования от модулей упругости достаточно гладкая [9,10]. В связи с этим отсутствует необходимость использовать сети с громоздкой архитектурой. Целью исследования было найти простую архитектуру сети, обеспечивающую решение задачи с приемлемой точностью и вместе с тем чувствительную к варьированию как входных, так и выходных параметров. Рассматривались сети двух видов: полутораслойный предиктор [1,3] с итерационным наращиванием объема и двухслойный перцептрон [4].

В нейросетевой модели на базе полутораслойного предиктора аппроксимируемая функция от входных переменных представлялась в виде частичной суммы сходящегося ряда.

.

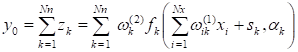
Составляющая ряда является выходомго потока сети. Особенность сети данного типа в том, что каждый последующий поток добавляется только после обучения предыдущего. В качестве входных параметров сети рассматривались модули упругости материалов основных слоев конструкции. В качестве выходов — характеристики динамического деформирования, полученные с помощью экспериментальных средств и методов [9,10].

Параметры сети определяются из условия минимума функции ошибок.

.

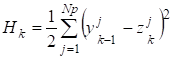
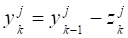
где? число потоков в сети;? число входов;? число точек (образцов), в которых задаются значения аппроксимируемой функции; ?ошибка аппроксимацииго потока дляго образца;? активационные функции.

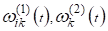
Параметры сети — коэффициенты синоптических связей и параметры активационных функций рассчитывались из условия минимума функции ошибок с помощью процедуры обратного распространения [5−7] по итерационным формулам :

,.

,.

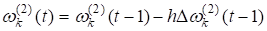
где? номер итерации.

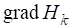
Поправки, ,, , выражались через проекции на соответствующие оси по формулам:

=;

=;

=;

=.

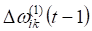
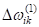
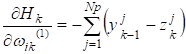
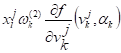
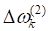
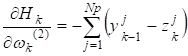
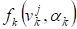
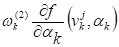
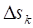
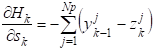
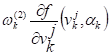
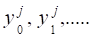
Как показали исследования, эффективность аппроксимации определяется не только архитектурой сети, но и корректным заданием начальных значений параметров сети, типом активационных элементов. Для упрощения анализа влияния входных данных на результаты расчетов входные параметры и выходы сети нормировались. Значения выходов для аппроксимируемой функций переводились в диапазон :

.

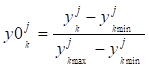
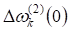
Входные параметры выбирались как случайные, равномерно распределенные точкимерного единичного куба. Значения входов и начальные значения параметров сети, ,, , согласовывались так, чтобы обеспечить попадание на активный участок активационной функции.

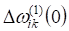
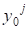
Особенности архитектуры сети с итерационным наращиванием объема таковы, что для каждого следующего потока в качестве требуемого выхода берется ошибка аппроксимации предыдущего потока. Эта функция является менее гладкой, чем функция выходов предыдущего потока. На Рис. 1 представлены графики аппроксимируемой и аппроксимирующей функций, зависящих от четырех входных параметров, полученные на первом шаге аппроксимации (для сети с одним потоком). Значения образцов изначально ранжированы по возрастанию. На Рис. 2 представлен график ошибки аппроксимации первого шага, которая является функцией выходов следующего добавляемого потока. Так как функция не является гладкой, для ее аппроксимации использовалась, кроме сигмоидной, синусоидальная активационная функция, с диапазоном изменения :

.

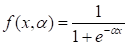
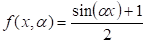
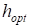
На скорости сходимости положительно сказалось варьирование параметров активационных функций; использование на каждой итерации процедуры автоматического выбора шага по заданным. При выполнении условия выпуклости функции ошибок.

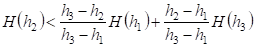
выбирался оптимальный шаг, при котором значение вычислялось в вершине параболы, соответствующей :

.

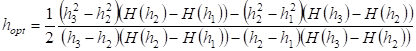
Рис. 1. Рис. 2.

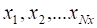
В нейросетевой модели на базе двухслойного перцептрона аппроксимируемая функция от переменных представлялась в виде суммы.

.

где.

? число нейронов выходного слоя,.

? выходго нейрона.

Параметры сети первоначально определялись из условия минимума функций ошибок.

.

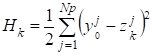
Затем они уточнялись путем минимизации функции.

.

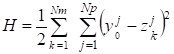
Сравнительный анализ результатов, полученных при использовании полутораслойного предиктора и двухслойного перцептрона показал возможность практического использования архитектур обоих типов для решения обратной коэффициентной задачи, однако двухслойный перцептрон при правильном подборе активационных элементов нейронов позволяет выполнять аппроксимацию при меньшем числе итераций.

Батурина Н. Ю. Нейросетевое моделирование в задачах исследования строительных конструкций // Инженерный вестник Дона. 2013. № 4.

Горбань А. Н. Обобщенная аппроксимационная теорема и вычислительные возможности нейронных сетей // Сибирский журнал вычислительной математики. 1998. Т. 1. № 1. С. 12−24.

Доррер М. Г. Аппроксимация многомерных функций полутораслойным предиктором с произвольными преобразователями. Методы нейроинформатики // Методы нейроинформатики. Красноярск: КГТУ, 1998. С. 130−151.

Максимова О. М. Разработка и применение нейросетевой технологии прогнозирования к задачам строительной механики и конструкций // Труды Междунар. Конгресса «Наука и инновации в строительстве» SIB — 2008. Воронеж: 2008. С. 146−151.

Абовский Н. П., Белобородова Т. В., Максимова О. М., Смолянинова Л. Г. Нейросетевые модели в задачах строительной механики // Изв. вузов. Строительство. 2000. № 7. С. 6−14.

Strategies in Structural Analysis and Design / Z. Peter Szewczyk. 2004.

Tsaregorodtsev V.G. Parallel implementation of back-propagation neural network software on SMP computers / Lecture Notes In Computer Science 3606 (PaCT-2005 Proceedings), Springer-Verlag. 2005. pp.185−192.

Жигульская Ю.И., Ляпин А. А Решение обратных задач строительной механики на основе нейронных сетей // Научное обозрение. 2014. № 10. Ч.2. С. 441−445.

Кадомцев М.И., Ляпин А. А., Шатилов Ю. Ю. Вибродиагностика строительных конструкций // Инженерный вестник Дона. 2012. № 3.

Кадомцев М.И., Ляпин А. А., Тимофеев С. И. К вопросам построения эффективных алгоритмов расчета системы «сооружение-грунт» // Инженерный вестник Дона. 2012. № 1.

References.

Baturina N. Ju. Inћenernyj vestnik Dona (Rus), 2013, № 4.

Gorban' A.N. Sibirskij zhurnal vychislitel’noj matematiki. 1998. T. 1. № 1. pp. 12−24.

Dorrer M.G. Metody nejroinformatiki. Krasnojarsk: KGTU, 1998. pp. 130−151.

Maksimova O.M. Trudy Mezhdunar. Kongressa «Nauka i innovacii v stroitel’stve» SIB. 2008. Voronezh: 2008. pp. 146−151.

Abovskij N. P., Beloborodova T. V., Maksimova O. M., Smoljaninova L. Izv. vuzov. Stroitel’stvo. 2000. № 7. pp. 6−14.

Strategies in Structural Analysis and Design. Z. Peter Szewczyk. 2004.

Tsaregorodtsev V.G. Lecture Notes In Computer Science 3606 (PaCT-2005 Proceedings), Springer-Verlag. 2005. pp.185−192.

Zhigul’skaja Ju.I., Ljapin A.A. Nauchnoe obozrenie. 2014. № 10. Ch.2. pp. 441−445.

Kadomcev M.I., Ljapin A.A., Shatilov Ju.Ju. Inћenernyj vestnik Dona (Rus), 2012, № 3.

Kadomcev M.I., Ljapin A.A., Timofeev S.I. Inћenernyj vestnik Dona (Rus), 2012, № 1.