Использование средних величин и показателей вариации в коммерческой деятельности

После изучения главы 5 студент должен: знать

• • методику расчета среднего уровня вариационного ряда;
• • основы построения, расчета, анализа основных показателей вариации; уметь
• • производить оценку основных характеристик вариационного ряда: среднего значения, моды, медианы, размаха вариации, дисперсии, среднего квадратического отклонения, коэффициента вариации;

владеть

• навыками анализа вариационных рядов.

Основные показатели среднего уровня вариационного ряда

Единицы изучаемой совокупности обладают интересующим пае признаком в разной мере. Для каждой единицы совокупности данный признак принимает различные значения в зависимости от конкретных условий, в которых находится изучаемая единица совокупности, и от особенностей ее собственного развития. Несовпадение уровней одного и того же показателя у отдельных единиц совокупности называется вариацией признака.

Для выявления характера распределения единиц совокупности по варьирующим признакам, определения закономерности в этом распределении строят ряды распределения единиц совокупности по какому-либо варьирующему признаку.

Ряды распределения, построенные по количественному признаку, называются вариационными.

Конструктивно вариационный ряд состоит из двух столбцов: один столбец — значения варьирующего признака (х — варианты), второй — частоты (J — абсолютное число случаев данного варианта) или частости (w — относительная доля каждой частоты в общей сумме частот).

Напомним, что вариационные ряды по способу построения бывают дискретные и интервальные.

Характер распределения дискретного вариационного ряда можно показать графически в виде полигона распределения. По оси х откладывают варианты, а по оси у — частоты.

Пример 5.1. Распределение продавцов одного из спортивных магазинов по возрасту (лет) характеризуется данными, представленными в табл. 5.1.

Таблица 5.1

Распределение продавцов спортивного магазина по возрасту.

Построим полигон распределения продавцов магазина по возрасту. По оси х откладываем варианты — возраст продавцов, а по оси у откладываем частоты — количество продавцов данного возраста (рис. 5.1).

Рис. 5.1. Полигон распределения продавцов магазина по возрасту Характер распределения интервального вариационного ряда можно показать графически в виде гистограммы распределения. Для интервального ряда с равными интервалами на оси х откладывают отрезки, равные длине интервала. На этих отрезках, как на основаниях, строят прямоугольники, высота которых пропорциональна частоте или частости. Для интервального ряда с неравными интервалами на оси ординат откладывают плотности распределения, так как в этом случае именно плотность распределения дает представление о заполненности каждого интервала. Площадь всей гистограммы численно равна сумме частот, или численности единиц в совокупности (если на оси ординат отложить частоты).

Ряды распределения могут изображаться в виде кумуляты накопленных частот. Накопленная частота показывает число единиц совокупности, у которых значение варианта не больше данного. Накопленная частота для данного варианта или для верхней границы данного интервала получается суммированием (накапливанием) частот всех предшествующих вариантов (интервалов), включая данный. Если вместо частот использовать частости, то аналогично получим накопленные частости. При графическом изображении кумуляты по оси х откладывают варианты ряда, а затем в этих точках выстраивают перпендикуляры, длина которых равна величине накопленных частот в верхних границах интервалов.

Пример 5.2. Распределение сотрудников малого предприятия, но величине заработной платы представлено в табл. 5.2.

Таблица 5.2

Распределение сотрудников малого предприятия по величине заработной платы.

Гистограмма распределения представлена на рис. 5.2.

Рис. 5.2. Гистограмма распределения сотрудников малого предприятия, но величине заработной платы.

Построим кумуляту распределения. По оси х откладываем величину заработной платы. По оси у при значении х, равном верхней границе интервала, откладываем накопленную частоту данного интервала (рис. 5.3).

Рис. 53. Кумулята распределения сотрудников малого предприятия, но величине.

заработной платы Как отмечалось выше, в статистике применяются различные виды средних величин.

Рассмотрим степенные средние.

В зависимости от характера имеющихся данных степенные средние могут быть простыми или взвешенными. В тех случаях, когда расчет осуществляется по несгруппированным данным, используется простая средняя. Но чаще при расчете средних величин отдельные значения осредняемого признака могут повторяться, встречаться по несколько раз. В подобных случаях расчет средней производится по сгруппированным данным или вариационным рядам. В этих случаях рассчитывают взвешенные средние.

Самым распространенным видом средней является средняя арифметическая. Расчет средней арифметической осуществляется по следующим формулам.

Средняя арифметическая простая.

где п — число вариант.

Средняя арифметическая взвешенная.

В отдельных случаях веса могут быть представлены не абсолютными, а относительными величинами — частостями. При замене частот на частости средняя величина характеристики не изменится, а формула примет вид.

n.

При этом упрощаются расчеты, так как составляет единицу, или 100%. ⁱ⁼¹

Рассмотрим сначала простую среднюю арифметическую.

Пример 5.3. Каждая партия изделий, выпускаемых предприятием содержит 1000 изделий. Задень было произведено 10 партий. При проведении контроля качества были получены следующие данные (табл. 5.3).

Таблица 53

Число бракованных изделий в партии для примера 5.3.

Рассчитаем среднее число бракованных изделий в партии:

Таким образом, в среднем каждая партия содержит пять бракованных изделий. Иными словами, уровень брака составляет пять изделий на тысячу, или 0,5%.

Пример 5.4. Предположим, что за день производится 120 партий. В данном случае вычислить среднее число бракованных изделий удобнее по сгруппированным данным (табл. 5.4).

Таблица 5.4

Число бракованных изделий в партии для примера 5.4.

Тогда.

или на основе данных столбца 3 табл. 5.4.

В ряде случаев роль весов при исчислении средней играют какие-либо другие величины. Например, при исчислении средней урожайности правильным будет взвешивание по размеру посевной площади, а не, но числу участков.

Пример 5.5. В табл. 5.5 приведено распределение 15 хозяйств по урожайности подсолнечника.

Таблица 5.5

Распределение хозяйств по урожайности подсолнечника.

Рассчитаем среднюю урожайность подсолнечника:

Как очевидно, в числителе формулы стоит общий валовый сбор подсолнечника, а в знаменателе — общая посевная площадь.

Таким образом, вопрос о весах, которые должны быть приняты при исчислении средней, определяется исходной информацией.

Часто вычисление средних величин приходится производить и по данным, сгруппированным в виде интервальных рядов распределения.

Пример 5.6. Провели группировку предприятий региона по объему товарооборота, данные представлены в табл. 5.6.

Таблица 5.6

Распределение предприятий региона по объему товарооборота.

Для вычисления средней величины надо в каждом интервале определить серединное значение х[, после чего произвести взвешивание обычным порядком. В закрытом интервале серединное значение определяется как полусумма значений верхней и нижней границ. Величины открытых интервалов (первого и последнего) условно приравниваются к величинам интервалов, примыкающих к ним (второго и предпоследнего). Таким образом, объем товарооборота в среднем на одно предприятие составит

При расчете статистических показателей помимо средней арифметической могут использоваться и другие виды средних. Однако в каждом конкретном случае в зависимости от характера имеющихся данных существует только одно истинное среднее значение показателя, являющееся следствием реализации его исходного соотношения.

Расчет средней гармонической осуществляется по следующим формулам.

Средняя гармоническая простая.

Средняя гармоническая взвешенная.

где V/ — веса для обратных значений Л).

Поясним приведенные формулы.

Для определения средней арифметической необходимо иметь ряд вариантов и частот, т. е. значения х, — и /₍. В некоторых случаях известны индивидуальные значения признака х, и произведения х/, а частоты/_; неизвестны. Чтобы рассчитать среднюю, обозначим произведение V-, = fx_jt от;

^Vi куда и =—.

х, Теперь преобразуем формулу средней арифметической таким образом,.

— УV•.

чтобы по имеющимся данным х и V исчислить среднюю: х = =

L/i ?Yl.

X,;

Средняя в такой форме называется средней гармонической взвешенной.

Средняя гармоническая простая используется значительно реже. Она может использоваться вместо взвешенной в тех случаях, когда значения V, для единиц совокупности одинаковы или равны единице.

Итак, выбор вида средней арифметической или гармонической обусловлен наличием исходных данных. Если имеются данные для числителя, применяют среднюю гармоническую, если для знаменателя — среднюю арифметическую.

Пример 5.7. Товар А реализуется на двух оптовых рынках. Предположим, имеются следующие данные (табл. 5.7).

Таблица 5.7

Средние цены оптовых рынков на товар А для примера 5.7.

Определим среднюю цену данного товара по двум оптовым рынкам, вместе взятым. В данном случае для расчета средней цены надо применить среднюю гармоническую (нам известен числитель — выручка от продаж, а знаменатель — объем продаж — надо найти):

Пример 5.8. Изменим исходные данные предыдущего примера (табл. 5.8).

Таблица 5.8

Средние цены оптовых рынков на товар А для примера 5.8.

Теперь нам известен знаменатель — объем продаж, а числитель следует найти. Применим среднюю арифметическую:

В основе вычислений ряда сводных расчетных показателей лежит средняя квадратическая. Наиболее широко этот вид средней используется при расчете показателей вариации. Расчет средней квадратической осуществляется по следующим формулам.

Средняя квадратическая простая.

Средняя квадратическая взвешенная.

В статистическом анализе также применяются степенные средние 3-го и более высоких порядков.

Для характеристики структуры совокупности применяются структурные средние. Как уже говорилось, наиболее часто в экономической практике применяются такие структурные средние, как мода и медиана.

Мода — наиболее часто встречающееся значение признака. Мода используется, например, при изучении покупательского спроса (при определении размеров одежды и обуви, пользующихся наибольшим спросом у покупателей), при анализе цен (фиксируя средние цены товаров или продуктов на рынке, записывают наиболее часто встречающуюся цену на тот или иной товар — моду цены) и т. д.

Для дискретного ряда мода находится непосредственно, но определению.

Для интервального ряда с равными интервалами сначала определяется модальный интервал, которому соответствует максимальная частота. Внутри модального интервала значение моды определяется по формуле.

где х₀ — нижняя граница модального интервала; h — длина модального интервала; f_Mo — частота модального интервала;Лго-i ^— частота интервала, предшествующего модальному; /_iWo+1 — частота интервала, следующего за модальным.

Для интервального ряда с неравными интервалами модальный интервал определяется по наибольшей плотности распределения. Строго говоря, мода — это значение признака, которому соответствует максимальная плотность распределения. Поэтому в формуле моды (5.1) вместо частот fMo ' fMo -1 > fMo+1 следует взять плотности распределения у_Мо, у_Мо__х, у_МоП.

Можно рассчитать как абсолютную, так и относительную плотность распределения. Абсолютная плотность распределения — это частота, при;

[

ходящаяся на единицу длины интервала, т. е. т¹, а относительная плот-

k

ность распределения — это частость, приходящаяся на единицу длины ин;

Щ

тервала, т. е. —^L.

hj

Графически моду определяют по гистограмме распределения. Для того чтобы определить моду, па гистограмме берут самый высокий прямоугольник, который и является модальным, далее верхнюю правую вершину модального прямоугольника соединяют с верхней правой вершиной предшествующего прямоугольника, а верхнюю левую вершину модального прямоугольника — с верхней левой вершиной последующего прямоугольника. Абсцисса точки пересечения этих отрезков и будет модой распределения. Рассмотрим определение моды в дискретном ряду.

Пример 5.9. В табл. 5.8 приведены данные о сроках погашения задолженностей по коммерческому кредиту.

Таблица 5.8

Статистическая оценка сроков погашения задолженностей по коммерческому кредиту.

Мода отражает наиболее часто встречающееся значение признака в вариационном ряду. Из приведенного вариационного ряда очевидно, что наиболее часто встречающейся величиной, т. е. модой этого ряда, является срок оплаты 18 дней (частота — 37 случаев наблюдения).

Рассмотрим определение моды в интервальном ряду.

Пример 5.10. В табл. 5.9 приведены данные о числе рабочих па предприятиях региона.

Таблица 5.9

Распределение предприятий, но числу рабочих.

Модальным интервалом является интервал с наибольшей частотой. Из приведенного вариационного ряда очевидно, что наибольшая частота (18) соответствует интервалу 500—600. Это означает, что чаще всего встречаются предприятия с численностью рабочих от 500 до 600 чел. Данный интервал и является модальным. Внутри модального интервата значение моды определяется по формуле (5.1):

Следовательно, из этой группы наиболее типичным является предприятие с численностью рабочих 567 чел.

Определим моду для этого вариационного ряда графическим способом. Для этого необходимо построить гистограмму распределения. Гистограмма представлена на рис. 5.3. Выбираем самый высокий прямоугольник, который и является модальным. Его верхнюю правую вершину соединяем с верхней правой вершиной прямоугольника, предшествующего ему, а верхнюю левую вершину — с верхней левой вершиной прямоугольника, следующего за ним. Абсцисса точки пересечения этих отрезков и будет модой распределения.

Рис. 5.4. Гистограмма распределения.

Таким образом, графически мы также получили значение моды 567 чел.

Медиана — значение варьирующего признака, приходящегося на середину ранжированной совокупности. Таким образом, в ранжированном ряду распределения одна половина ряда имеет значения признака меньше медианы, а вторая — больше медианы.

В дискретном ряду медиана находится непосредственно на основе накопленных частот.

Для интервального ряда сначала определяется медианный интервал. Медианному интервалу соответствует первый из интервалов, для которого накопленная сумма частот превышает половину общей совокупности наблюдений. Внутри найденного интервала медиана находится по формуле.

где х₀ — нижняя граница медианного интервала; h — длина медианного интервала; f_Me — частота медианного интервала; F_Me__{ — накопленная частота интервала, предшествующего медианному.

В интервальном ряду медиану можно определить графически по кумуляте. Для определения медианы по кумуляте из точки на шкале накопленных частот (частостей), соответствующей номеру медианы, проводится прямая, параллельная оси абсцисс, до пересечения с кумулятой. Затем из точки пересечения указанной прямой с кумулятой опускается перпендикуляр на ось абсцисс. Абсцисса точки пересечения и является медианной.

Пример 5.11. Найдем медиану для дискретного вариационного ряда, представленного в табл. 5.8. Общее число случаев наблюдения 150. Для определения медианного значения признака по следующей формуле находят номер медианной единицы ряда:

где N — объем совокупности.

Следовательно, номер медианы для нашего ряда =75,5. Полученное дробное значение, всегда имеющее место при четном числе единиц в совокупности, указывает, что точная середина находится между 75-м и 76-м случаями наблюдения. Накапливаем частоты до тех пор, пока не будет превзойден номер медианы. Представим результаты расчета в табл. 5.10.

Таблица 5.10

Статистическая оценка сроков погашения задолженностей, но коммерческому кредиту.

Итак, в 33 случаях срок оплаты составлял не более 10 дней, в 62 случаях — не более 14 дней, в 87 случаях — не более 15 дней. То есть в 63-м, 64-м,…, 86-м, 87-м случаях срок оплаты составлял 15 дней, значит, 75-й и 76-й случаи наблюдения находятся в этой группе. Таким образом медиана данного ряда равна 15.

Пример 5.12. Рассмотрим определение медианы в интервальном ряду, представленном в табл. 5.9. Прежде всего найдем медианный интервал. Для определения медианного интервала необходимо определять накопленную частоту каждого последующего интервала до тех пор, пока она не превысит 1 /2 суммы накопленных частот. В нашем случае общее число предприятий 55, следовательно, номер медианы = 28.

На основании накопленных частот (табл. 5.11) определяем, что 28-е предприятие находится в интервале 500—600.

Таблица 5.11

Распределение предприятий по числу рабочих.

Точное нахождение медианы на данном интервале осуществляется по формуле (5.2):

Таким образом, на 50% предприятий число рабочих меньше 536 чел., а на 50% предприятий — больше.

Определим медиану для этого вариационного ряда графическим способом. Для этого необходимо построить кумуляту (рис. 5.5). Из точки на шкале накопленных частот, соответствующей частости, равной 50%, проводится прямая, параллельная оси абсцисс, до пересечения с кумулятой. Из точки пересечения указанной прямой с кумулятой опускается перпендикуляр на ось абсцисс. Абсцисса точки пересечения и является медианной.

Рис. 5.5. Кумулята для примера 5.11.

Таким образом, мы тоже получили значение медианы 536 рабочих.

Если мода отражает типичный, наиболее распространенный вариант значения признака, то медиана практически выполняет функции средней для неоднородной, не подчиняющейся нормальном закону распределения совокупности. Она также используется в тех случаях, когда средняя нс позволяет объективно оценить исследуемую совокупность вследствие сильного влияния максимальных и минимальных значений. Проиллюстрируем познавательное значение медианы следующим примером.

Пример 5.13. Допустим, нам необходимо дать характеристику заработной платы группы людей, насчитывающей 100 чел., из которых 99 имеют заработную плату в интервале от 100 до 400 долл, в месяц, а заработная плата последнего составляют 50 000 долл. (табл. 5.12).

Таблица 5.12

Распределение служащих по заработной плате.

Если мы воспользуемся средней арифметической, то получим среднюю заработную плату, равную.

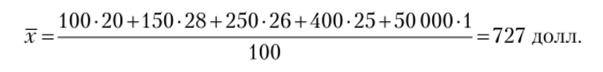
Средняя заработная плата не только в несколько раз меньше заработной платы 100-го человека, но и имеет мало общего с заработной платой остальной части группы. Медиана же, равная в данном случае 250 долл., позволит дать объективную характеристику уровня заработной платы 99% данной совокупности людей. Мода, равная 150 долл., показывает, что больше всего сотрудников имеют заработную плату в размере 150 долл.

Какой из трех показателей (среднее, моду, медиану) следует использовать в конкретных обстоятельствах? Насколько эти три характеристики вариационного ряда отличаются между собой?

Если распределение близко к нормальному, то разница небольшая, поскольку каждая из характеристик стремится к четко выраженной середине.

Однако в случае асимметричного распределения данных эти характеристики могут заметно различаться, как мы уже показали в предыдущем примере.

Среднее следует использовать, когда распределение набора данных близко к нормальному, поскольку в этом случае среднее является самой эффективной характеристикой. Среднее также следует вычислять и в тех ситуациях, где необходимо сохранить или предсказать общую сумму значений данных, так как другие характеристики не позволяют это сделать.

Медиана служит хорошей характеристикой асимметричного распределения, поскольку на нее не влияет небольшое число данных с высокими (или низкими) значениями. В случае сильной асимметрии медиана значительно лучше, чем среднее, характеризует большинство данных. Медиана полезна при наличии выбросов значений, так как она устойчива к их влиянию.

Моду используют, когда нужно определить наиболее распространенную категорию.

Помимо рассмотренных, существует много других характеристик.

К структурным средним также относятся квантили, или градиенты. Частными случаями квантилей являются квартили, квинтили и децили.

Квартилями называются такие значения признака, которые делят распределение на четыре равные части. Обозначим значения x-_v делящие вариационный ряд на четыре равные части, через Q_v Q_2j (2зНиже первой квартили Q_x лежит 25% значений х_г Ниже второй квартили Q₂ лежит половина значений x_jr т. е. вторая квартиль делит распределение пополам и совпадает с медианой. Между второй Q₂ и третьей Оз квартилями лежит 25% значений х, а оставшиеся 25% значений х_г лежит выше третьей квартили ОзОз называется верхней квартилыо, Qj — нижней квартилыо.

Квинтили делят распределение на пять равных частей, децили — на десять.

Одной из областей, в которых используются квантили распределения, является управление рисками. В экономических системах в условиях риска, когда неопределенность носит вероятностный характер, а потери описываются случайной величиной, минимизация риска может состоять, в частности, в минимизации квантиля распределения (например, минимизации квантиля порядка 0,95, выше которого располагаются большие потери, встречающиеся крайне редко (в нашем примере — в пяти случаях из ста)). Данный подход нацелен на минимизацию больших потерь, на защиту от разорения. При таком подходе средние потери могут увеличиваться, зато максимальные будут контролироваться.

В ряду квантильных мер риска можно выделить такой показатель, как value-at-risk (VAR). Утверждение о том, что портфель имеет определенное значение VAR, фактически означает следующее: в течение промежутка времени Т с доверительной вероятностью Р абсолютная величина убытка по портфелю не может быть больше, чем VAR (доход по портфелю не может быть меньше -VAR), при этом абсолютная величина убытка, превосходящая VAR, также не исключена, однако такой убыток может случиться лишь с малой вероятностью (1 ~Р). Представляется целесообразным рассчитывать эти величины одновременно для нескольких различных значений доверительной вероятности Р (например 0,950; 0,975; 0,990; 0,999). Показатель VAR используется в риск-менеджменте в качестве базы для лимитов по открытым позициям, для расчета достаточности капитала, оценки стоимости портфеля, оценки доходности с учетом риска и т. д.