Колебания струны. 
Курс общей физики

Натянутая тонкая струна в равновесном состоянии имеет форму прямой линии. Направим ось х вдоль этой прямой (рис. 13.6). В таком случае положение произвольной точки Р струны удобно определить при помощи координаты х. Если каким-либо образом вывести струну из состояния покоя, то она начнет совершать довольно сложные движения, называемые колебаниями струны. В процессе колебаний положение точки Р будет изменяться с течением времени. Пусть в момент времени t

эта точка оказалась в положении Р'. Вектор? = РР', начало которого находится в точке Р, а конец — в точке Р', характеризует положение рассматриваемой точки струны в произвольный момент времени. Этот вектор называют смещением.

Рис. 13.6. Колебания струны.

Процесс колебаний струны удобно описывать посредством зависимости вектора смещения? от времени t и координаты х произвольной точки струны:

Колебания струны называют поперечными, или волнами изгиба, если векторы смещения всех точек струны всегда направлены перпендикулярно к равновесному положению струны. Если же векторы смещения всегда направлены вдоль самой струны, то колебания называют продольными, или волнами сжатия. В общем случае по струне могут распространяться как волны изгиба, так и волны сжатия.

Исследуем поперечные колебания струны в плоскости ху. В этом случае проекции вектора смещения? на оси х и z будут равны нулю, и процесс колебаний можно будет описать одной функцией.

где у есть проекция вектора смещения на ось у. Составим уравнение для этой функции. Искомое уравнение будет иметь наиболее простой вид, если предположить, что струна совершает малые колебания. Это где.

— частная производная по х от функции (13.24).

Рассмотрим небольшой участок струны, который занимает отрезок [xi, Xj] оси х, когда струна покоится (рис. 13.7). При этом его длина равна dx = хj — В смещенном положении длина этого участка будет.

В силу условия (13.25) можно пренебречь квадратом производной у' но сравнению с единицей. Таким образом получим.

т.е. в принятом приближении удлинения участков струны в процессе колебаний не происходит. Вследствие этого согласно закону Гука модуль силы натяжения F в каждой точке струны будет всегда один и тот же.

Однако направление силы натяжения F будет изменятся от точки к точке и с течением времени.

Рис. Li. 7. Участок струны и действующие на него силы.

На рис. 13.7 показаны силы натяжения, которые действуют на концы выделенного участка струны. Проекция на ось у одной из этих сил равна.

где, а — угол между вектором силы и осью х. Тангенс угла а равен производной по х от функции у = y (t, х), которая определяет форму струны в произвольный момент времени:

где Применим второй закон Ньютона для рассматриваемого участка струны. В проекциях на ось у этот закон дает уравнение.

Из условия (13.25) следует, что угол а мал и его синус приближенно равен тангенсу этого угла:

При этом проекция F_y силы натяжения струны в точке х будет.

— масса участка струны длиной dx,.

— линейная плотность массы, т — масса струны, / - ее длина. Ускорение а_у есть вторая производная от координаты у = y (t, х) но времени:

где х € [х_ь х₂].

Найдем сумму сил в правой части уравнения (13.28) при помощи формулы (13.27). Изображенный на рис. 13.7 участок струны немного искривлен. Вследствие этого векторы F и F₂ не параллельны и их проекции на ось у в общем случае не равны по величине. Положим х = х. При этом для проекции на ось у силы натяжения F, которая действует на левый конец выделенного участка струны, можно записать выражение.

Так как х₂ = x-f dx, проекция на ось у силы натяжения F₂, действующей на правый конец участка, будет.

Таким образом, получим.

Выражение в круглых скобках есть приращение функции у'(*, я), которое равно произведению ее производной на дифференциал аргумента:

где Подстановка полученных выражений в равенство (13.28) приводит к уравнению.

которому можно придать вид.

где Сравним уравнения (13.3) и (13.29). Нетрудно видеть, что это есть уравнения одного типа. Так доказано, что малые поперечные колебания струны есть изгибные волны, которые распространяются по струне со скоростью (13.30). Для волн сжатия можно получить аналогичное уравнение.

Если концы струны закреплены в точках х = 0 и х = /, то решения волнового уравнения (13.29) должны удовлетворять следующим граничным условиям:

Нетрудно проверить, что функция.

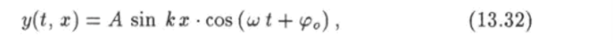
где А и <�р₀ — произвольные постоянные, является решением уравнения (13.29) и удовлетворяет первому из условий (13.31). Она будет удовлетворять также и второму условию, если волновое число принимает значения где n = 1, 2, 3, … Функция (13.32) описывает стоячие волны. Так как волновое число и длина волны связаны соотношением к = 2я*/А, из формулы (13.33) найдем, что в натянутой струне с закрепленными концами могут существовать только такие стоячие волны, для которых на длине / струны укладывается целое число полуволн:

Стоячие волны, описываемые функцией (13.32), показаны на рис. 13.8 для п = 1, 2 и 3.

Рис. 13.8. Стоячие изгибные волны в струне с закрепленными концами.

Зная волновое число и скорость волны, найдем частоту по формуле (13.6):

Согласно этой формуле частота колебаний струны тем выше, чем сильнее она натянута. Чем больше длина струны и ее масса, тем меньше частота.

Колебания струны, описываемые функциями (13.32), называют гармониками, а частоты ш_п% определяемые формулой (13.35), — собственными частотами колебаний струны. Колеблющаяся струна издает звук, т. е. создает распространяющиеся в воздухе упругие волны. Звук, издаваемый струной, когда в ней возбуждена только одна гармоника, называется простым тоном. Простой тон самой низкой частоты и> называют основным, а все другие * обертонами. Общее решение уравнения (13.29) колебаний струны с закрепленными концами представляет собой линейную комбинацию функций (13.32). Из этого следует, что колеблющаяся струна может одновременно издавать звуки разных частот. При этом тембр звука зависит от распределения энергии по гармоникам и определяется способом возбуждения колебаний струны.

В струне могут распространяться продольные волны, или волны сжатия. Если представить себе струну как цепочку атомов, то при распространении по этой цепочке продольной волны расположение атомов в некоторый момент времени будет примерно таким, как показано на рис.

13.9.

Рис. 13.9. Продольные волны в цепочке атомов.

13.9. Энергия колебаний струны Колеблющаяся струна обладает кинетической и потенциальной энергиями, которые обозначим Т и W соответственно. Полная механическая энергия струны 6 равна сумме этих энергий:

Кинетическая энергия участка струны от х до х + dx равна.

Кинетическая энергия всей струны равна сумме кинетических энергий отдельных ее участков:

Работа Акс консервативной силы равна разности потенциальных энергий тела до перемещения и после. Так работа А_Кс сил натяжения струны при ее перемещении из одного положения в другое будет где W и W2 - потенциальные энергии струны в положении 1 и в положении 2 соответственно. Пусть в положении 1 струна была в момент времени t, в положении 2 — в момент времени 12. Тогда первое положение струны будет описываться функцией y (t 1, х), а второе — функцией у (<2, г). Следовательно, энергия W должна зависеть некоторым образом от функции y (*i, х), а энергия W2 - таким же образом от y (t2, х).

Найдем работу А сил натяжения струны при ее перемещении из положения 1 в положение 2. На участок струны от х до х + dr действуют силы натяжения, сумма проекций которых на ось у равна.

Мощность есть произведение силы на скорость:

Мощность сил натяжения для всей струны равна интегралу от этого выражения:

Преобразуем этот интеграл методом интегрирования по частям. Пусть.

Тогда где Получим.

Первое слагаемое в этой формуле более подробно можно записать так:

Здесь F y'(t, /) есть проекция на ось у силы натяжения, которая приложена к концу струны, где х = /. Величина y (t, /) есть скорость этого конца струны. Следовательно, выражение F y'(t, /) y (t, I) есть мощность силы натяжения, приложенной к концу струны. Аналогично, выражение — F y'(t, 0) y (t, 0) есть мощность силы натяжения, приложенной к другому концу струны.

Работа равна интегралу от мощности по времени:

Первое слагаемое в этом выражении есть интеграл по времени. Оно содержит в себе функцию y (t, х) при всех t € [<2]• Другими словами, это слагаемое есть работа неконсервативных сил, которая зависит от пути, по которому струна переходит из положения 1 и положеие 2. Второе слагаемое зависит только от функций y (х) и у (<2, я), которые определяют положения 1 и 2 струны до и после перемещения. Следовательно, это есть работа консервативных сил, а выражение.

— потенциальная энергия струны в момент времени t, когда ее форма определяется функцией y (t, х).

Итак, полная механическая энергия струны в момент времени t будет.