Развитие интереса учащихся к математике через эстетический потенциал задач и теорем с чертежом

Специальные исследования по проблемам формирования познавательного интереса, проведенные Г. И. Щукиной, В. С. Ильиным, показывают, что интерес во всех его видах и на всех этапах развития характеризуется по крайней мере тремя обязательными моментами:

• — положительными эмоциями по отношению к деятельности;
• — наличием познавательной стороны этих эмоций;
• — наличием непосредственного мотива, идущего от самой деятельности.

Отсюда следует, что в процессе обучения важно обеспечивать возникновение положительных эмоций у учащихся по отношению к учебной деятельности, к ее содержанию, формам и методам осуществления. Интерес как средство обучения действует тогда, когда на первый план выступают внутренние стимулы, способные удержать интерес, возникающий у учащихся при внешних воздействиях. Новизна, необычность, неожиданность — все эти особенности, подчеркнутые при сообщении материала, способны не только вызвать интерес, но и побудить эмоции, порождающие желание изучать материал более глубоко [4].

Исследования педагогов и психологов показали, что в подростковом возрасте особенно значимым фактором в развитии интереса к учению является содержание учебного предмета. Средствами, связанными с содержанием учебного материала, побуждающими формирование мотивации учения, могут быть следующие:

• — практическая значимость изучаемого материала для ученика;
• — доступность учебного материала;
• — новизна;
• — исторические факты;
• — наглядность и занимательность материала.

Выделенные параметры математических способностей, а также поиск эффективных средств позволили выделить исторические задачи и теоремы с чертежом, сыгравшие важную роль в историческом развитии математики и ее методики преподавания.

Использование исторического материала при обучении математике предполагает внедрение новых форм и методов. Для полноты восприятия этого материала необходимо, чтобы каждый был вовлечен в процесс творческой, поисковой деятельности.

С этой целью целесообразно использование технологии укрупнения дидактических единиц, которая предполагает изучение «дидактического окружения» исторической теоремы [5]. Исследование одной теоремы позволяет понять механизм ее появления, процесс поиска различных способов ее доказательства, механизм ее применения, процедуру обобщения утверждений. Первый трактат шотландского философа эпохи Просвещения Фрэнсиса Хатчесона «О красоте, порядке, гармонии, целесообразности» начинается словами: «Красота теорем, или доказательств правильности всеобщих истин, заслуживает отдельного рассмотрения, поскольку по природе своей она значительно отличается от ранее рассмотренных видов красоты; и, однако, нет такой другой, в которой мы могли бы увидеть такое поразительное разнообразие при единообразии… У теорем есть ещё одна красота, которую нельзя обойти и которая состоит в том, что одна теорема может содержать огромное множество следствий, которые легко из неё выводятся…» [2].

Для формирования устойчивого интереса к математике, а также эстетического воспитания на уроках математики через исторические задачи и теоремы мы предлагаем следующие критерии их отбора: доступность для учащихся, соответствие с программным материалом, возможность построения чертежа, возможность его параметризации для фронтальной работы в классе, перспектива выхода в пространство.

Рассмотрим две задачи, которые на наш взгляд, отвечают всем этим критериям. Они привлекают еще и тем, что их разделяют века, а это возможность почувствовать, что элементарная математика является частью живого древа математики всех прошлых и будущих времен.

Задача «Луночки Гиппократа»

Пытаясь решить эту задачу античности, нашли квадрируемые фигуры, ограниченные кривыми линиями. Мы имеем здесь в виду луночки (мениски) Гиппократа Хиосского, образованные дугами окружностей. Гиппократ нашел три вида луночек [1]. Советские ученые Н. Г. Чеботарев и А. В. Дороднов в 30−40-х годах доказали, что имеется пять видов квадрируемых луночек, но ни одна из них не квадрируема вместе с кругом. Если рассмотреть при изучении тем «Окружность и круг», «Теорема Пифагора», «Длина окружности и площадь круга» луночки Гиппократа, то это вызовет удивление и интерес своей необычной формой и свойствами. Дело в том, что луночки — это криволинейные фигуры и тем не менее их площадь равна площади прямолинейной фигуры. Благодаря своей увлекательности изучение этого материала можно продолжить на внеклассных занятиях.

Для формирования самостоятельной работы и в этой связи активизации познавательной деятельности учащихся, без которой немыслимо развитие познавательного интереса, по наглядному чертежу можно организовать самостоятельную работу на заполнение коллективной таблицы.

r_впис=(а+в-с)/2.

r_лун=(а+в-с)/4.

r^*=а+в-с изюминка Ч. Тригга.

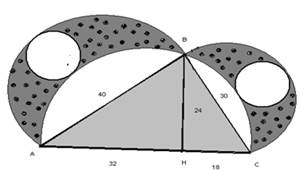
Рис. 1.

Таблица 1

По завершению работы учащиеся делают вывод, что площадь двух луночек равна площади треугольника. Кстати, у этой фигуры есть еще одно замечательное свойство и в этом можно убедиться при построении и вычислении: луночки имеют одинаковую ширину. Точнее говоря, диаметры наибольших вписанных в них окружностей равны каждый половине разности между суммой катетов и гипотенузой треугольника.

Теорема Содди

Среди многих математических открытий 20 века, в смысле близости этого открытия к понятиям элементарной (школьной) геометрии, особое место принадлежит открытию Ф. Содди теоремы о взаимосоприкасающихся окружностях и сферах.

Включение теоремы Содди в курс элементарной и аналитической геометрии имеет следствием обогащение фонда упражнений, позволяющих обеспечивать сочетание координатного метода с вычислениями и контроль точных построений измерениями и вычислениями.

Исключительно ценно в этих упражнениях воспитание через них эмоционального удовлетворения от постижения глубинной красоты математических теорем. Теорема весьма богата прямыми и опосредованными логико-психологическими связями со многими базисными понятиями математики: касание прямой с окружностью, касание двух и более окружностей, формула Герона и т. д.

В формулировке Содди теорема состоит из двух утверждений:

1. Сумма квадратов значений кривизны четырех взаимно соприкасающихся окружностей равна половине квадрата суммы значений кривизны этих окружностей:

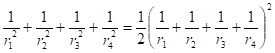
В символах кривизны эта формула будет иметь следующий вид:

(*).

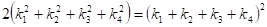
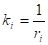
где — кривизна взаимосоприкасающихся окружностей.

2. Сумма квадратов значений кривизны пяти взаимосоприкасающихся сфер равна трети квадрата суммы значений кривизны этих сфер:

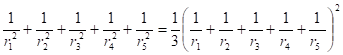
В символах кривизны эта формула будет иметь следующий вид:

(**).

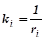
где — кривизна взаимосоприкасающихся сфер. [3].

Теорема Содди связывает значения радиусов пяти касающихся окружностей. Построение этих окружностей достаточно сложно для учащихся, но оно вполне доступно и полезно для студентов инженерных профессий. Для учащихся была организована групповая работа по нахождению r₄ и r₅.

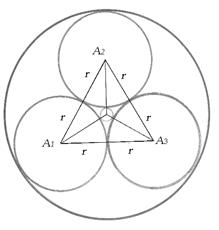
Рис. 2.

Таблица 2.

Включение формулы Содди в практикум по решению задач обогащает не столько ассортимент задач, сколько общепсихологическую культуру переработки информации.

Задача о построении окружности, касающейся трех заданных линий, является классической задачей (частным случаем проблемы Аполлония).

После освоения формул Содди в распоряжении учащихся оказываются три способа решения данной задачи, а именно: радиус окружности можно вычислить по формуле Содди, координатным методом, измерением при построении на миллиметровой бумаге. Наиболее ценный дидактический элемент в подобных ситуациях — это выполнение классического правила дидактики математики: лучше одну задачу решить несколькими способами, чем несколько задач одним способом.

Таким образом, для развития интереса учащихся к математике целесообразно включать в программный материал значимые, красивые исторические задачи с чертежом, при этом из всех конфигураций чертежа выбирать наиболее изящный. Подлинное математическое образование возможно лишь в случае полноценного раскрытия эстетического потенциала математики в процессе обучения.

познавательный интерес эстетический потенциал задача.

Примечания

• 1. Белозеров С. Е. Пять знаменитых задач древности. Ростов н/Д, 1975. 320 с.
• 2. Волошинов Н. В. Математика и искусство. М., 1992. С. 32.
• 3. Кокстер Г. С.М.

  Введение

  в геометрию. М., 1969. С. 31.

• 4. Щукина Г. И. Проблема познавательного интереса в педагогике. М., 1971. С. 13.
• 5. Эрдниев П. М. Укрупнение дидактических единиц как технология обучения: в 2 ч. М., 1992. 255 с.