Базовые модели временных рядов

Белый шум

Белым шумом называется процесс, имеющий постоянное математическое ожидание, постоянную дисперсию и нулевую, для всех, кроме нулевого лага, автоковариационную функцию. То есть 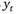- белый шум, если.

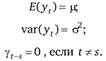
Белым шум, по определению, — слабо стационарный процесс. В самом деле, нулевая для всех, кроме нулевого лага, автоковариационная функция означает, что наблюдения не коррелированны между собой. График белого шума, смоделированного в пакете Eviews, изображен на рис. 8.3.

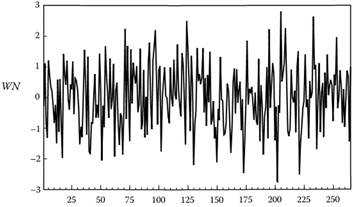
Рис. 8.3. Белый шум (модельный пример) Если к условиям стандартного белого шума добавить условие нулевого математического ожидания, получится белый шум с нулевым средним.

Если выполняется предположение о нормальном распределении процесса 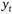, то процесс будет строго стационарным. Кроме того, коэффициенты автокорреляции также будут распределены согласно нормальному закону.

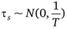
где 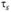 — коэффициент автокорреляции; Т — размер выборки.

Случайное блуждание

Случайным блужданием называется процесс, описываемый уравнением.

(8.3).

где 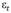- белый шум.

Это просто авторегрессия первого порядка, с единичным коэффициентом. Модель случайного блуждания можно представить как.

Таким образом, модель случайного блуждания выражается через начальное значение и сумму белых шумов (рис. 8.4). Математическое ожидание такого процесса равняется начальному значению:

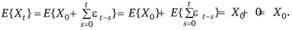
Дисперсия случайного блуждания при условии некоррелированност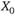и и имеет вид.

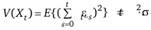
Поскольку, как очевидно из уравнения, дисперсия зависит от времени, следовательно, условие постоянства дисперсии не выполняется и случайное блуждание не является стационарным процессом.

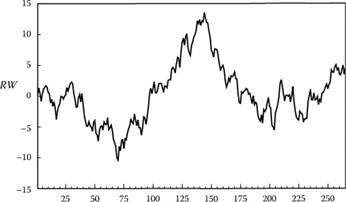
Рис. 8.4. Случайное блуждание (модельный пример) Для того чтобы привести случайное блуждание к стационарному ряду, нужно просто взять первую разность То есть 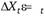, при этом  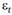— белый шум, слабо стационарный процесс. Прием взятия разностей очень часто встречается в эконометрике, на нем основывается один из принципов модели ARIMA, которая будет рассматриваться позже.

Модель скользящей средней

Модель скользящей средней — одна из простейших моделей временных рядов. В модели в качестве объясняющих переменных выступает комбинация белых шумов (рис. 8.5). То есть ряд 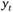описывается процессом ?? (?), если.

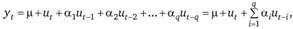(8.4).

где (при ) — белый шум, с нулевым математическим ожиданием и дисперсией .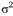

Уравнение может быть переписано с помощью оператора сдвига. В самом деле, если , то уравнение (8.4) можно представить как ,.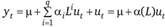

где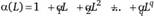

Рис. 8.5. (модельный пример) Найдем характеристики процесса скользящей средней:

Таким образом, процесс скользящей средней имеет постоянные математическое ожидание и дисперсию и ненулевую до ?-го лага автоковариацию.

Авторегрессионная модель

В основе авторегрессионных моделей (рис. 8.6) лежит предположение о том, что последующие значения рассматриваемой переменной зависят только от ее значений в предыдущие периоды и ошибки. Таким образом, авторегрессионная модель порядка 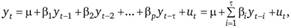записывается следующим образом:

(8.5)

где 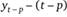 — белый шум, 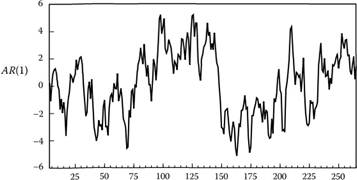-й лаг рассматриваемой переменной.

Рис. 8.6. (модельный пример) Кроме того, уравнение авторегрессионной модели может быть записано с использованием оператора сдвига:

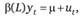
или.

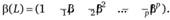
Где

При работе с процессом AR необходимо первым делом проверить его стационарность. Дело в том, что в моделях, где коэффициенты не удовлетворяют условиям стационарности, будет наблюдаться незатухающее влияние предыдущих значений ошибок на текущее значение параметра, что усложняет процесс оценивания подобной модели.

Для того чтобы вывести условие стационарности для авторегрессионных процессов, воспользуемся следующей формой записи модели AR:

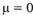
Пусть , тогда.

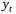
Процесс будет стационарным, если его можно представить в виде.

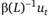
На самом деле, может быть представлено в виде МА (оо) процесса 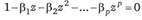. Причем, если авторегрессионный процесс стационарен, то коэффициенты МА (со) будут уменьшаться для последующих лагов, а если процесс не стационарен, то коэффициенты МА (со) не будут сходиться к нулю по мере увеличения порядка лага.

Таким образом, условие стационарности AR (q) процесса заключается в том, чтобы корни характеристического уравнения.

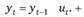
были по модулю больше единицы.

Рассмотрим условие стационарности авторегрессионного процесса на примере модели случайного блуждания.

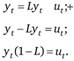
Первым делом перепишем модель случайного блуждания с помощью оператора сдвига:

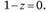
Характеристическим уравнением для процесса случайного блуждания будет уравнение вида.

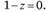
Единственный корень характеристического уравнения z = 1 не является по модулю большим единицы. Следовательно, процесс случайного блуждания не является стационарным процессом.