Методико-математические основы обучения математике в начальной школе

В результате изучения данной главы студент должен: знать

• • содержание основных разделов курса математики начальной школы;
• • объем и содержание математических понятий, изучаемых в начальной школе;
• • связи и зависимости между математическими понятиями;
• • место каждого понятия в системе обучения математике; уметь
• • раскрыть содержание каждого понятия для младших школьников;
• • представить каждое из изучаемых математических понятий знаками различных семиотических систем, в том числе знаками визуальной семантики;

владеть

• • технологиями обучения математическому понятию, в том числе ИКТ;
• • методами, приемами, способами раскрытия содержания каждого из изучаемых понятий.

Онтологически значимые теоретические модели натуральных чисел в начальном математическом образовании

Конструктивная теория Гильберта

Вопросы для обсуждения

• 1. Какие функции натуральных чисел должны отражаться в начальном математическом образовании?
• 2. Почему методической науке потребовалось выяснение сущности натурального числа? Каковы связи между уяснением природы натурального числа и методикой обучения арифметике?
• 3. Что диктует методике обучения арифметике кш 1струkthbi 1ая теория Гил ьберта?
• 4. Как связаны теоретические установки конструктивной теории Гильберта с интуитивными представлениями младших школьников о натуральном числе?

Стержнем курса математики начальной школы является арифметика натуральных чисел. Методика преподавания математики в начальной школе должна исходить из четкого понимания природы натурального числа. История математики свидетельствует: на протяжении тысячелетий вопрос о том, что такое натуральное число, не возникал. Натуральные числа рассматривались исключительно с точки зрения их функциональных возможностей как инструмент счета, измерения, или как элемент некоторой последовательности знаков.

Необходимость уточнения понятия числа была вызвана развитием анализа и сложившимся на рубеже XIX—XX вв. взглядом, что убедительная картина математики может быть построена на теоретико-множественной основе. В это же время усилиями многих выдающихся математиков было установлено, что арифметика натуральных чисел образует фундамент всего грандиозного здания математики. На теоретико-множественной основе Г. Грассман, Р. Дедекинд, Дж. Пеано, Д. Гильберт, Г. Кантор разработали ряд теоретических моделей натуральных чисел. С точки зрения дидактики знания об этих моделях являются существенной составляющей проектирования системы обучения, не только не противоречащими разработанным теориям, но и определяющими возможности его построения так, чтобы изучаемые факты были поняты детьми и осмыслялись как несомненно доказанные. Во второй главе было показано, что с большим или меньшим успехом курс математики начальной школы может быть выстроен либо дедуктивно (В. В. Давыдов), либо индуктивно (М. И. Моро), либо сочетая оба способа в зависимости от конкретной темы и связей ее с предшествующим и последующим материалом (Л. Г. Петерсон). То, что, с одной стороны, число существует только как идеальный мыслимый понятийный образ, а с другой — недостаточность как житейского, так и математического опыта ребенка, опора на который могла бы способствовать формированию умений создавать такие образы и оперировать ими, данную методическую задачу делает исключительно трудной. Необходимым условием ее решения является анализ теоретических моделей натуральных чисел, разработанных выдающимися математиками.

Д. Гильберт и П. Бернайс исследовали возможность теоретического построения арифметики как результата мысленных экспериментов над объектами, которые предполагаются конкретно заданными (Д. Гильберт, П. Бернайс, 1982). В качестве исходного объекта берется объект «I», называемый цифрой. Операция порождения других объектов состоит в приписывании этой цифры к уже имеющимся (в практике обучения младших школьников цифре может сопоставляться палочка из набора счетных палочек, используемых как наглядное средство, а операции порождения — взятие еще одной палочки). Полученные в результате такой операции объекты также называются цифрами. Наряду с цифрами вводятся в рассмотрение некоторые другие знаки, знаки-«сообщения», относительно которых предполагается, что они могут быть однозначно опознаны:

• • строчные латинские буквы для обозначения произвольных нефиксированных цифр;
• • обычные знаки для сокращенной записи цифр;
• • знаки для конкретных процессов построения и для арифметических операций, с помощью которых из исходных цифр получаются новые;
• • знаки «>» и «<�» для обозначения отношений порядка между цифрами, знак «=» для сообщения о графическом равенстве двух цифр;
• • скобки в качестве знаков для указания порядка действий.

Пусть а и b — различные цифры. Обе они начинаются с цифры I, построение каждой из них будет протекать одинаково до тех пор, пока для одной из них построение не оборвется, в то время как для другой будет продолжаться. Когда этот момент наступит, одна из цифр совпадет с частью другой.

Если цифра а совпадает с частью цифры А, то будем говорить, что а < b, или, что-то же самое, b > а. Из наглядного смысла этих отношений видно, что одно из них исключает другое, причем всегда имеет место одно и только одно из соотношений:

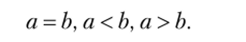
Но также дети сравнивают упорядоченные совокупности объектов любой природы. Например, ситуация, изображенная на рисунке.

приводит к записи результата сравнения К > 3 (кружочков больше, чем звездочек), различное обозначение исходных элементов не меняет сути дела, но становится легко воспринимаемым.

В тесной связи с отношением порядка цифр находится операция сложения. Если имеются цифры awb, то цифра с, которая получается присоединением I к а так, что цифра I, которой начинается 6, будет приписываться вслед за цифрой I, которой оканчивается а, гем же самым способом как если бы продолжалась операция порождения. Такой способ объединения цифр назовем сложением и для его обозначения применим знак «+». Другими словами, если, например,.

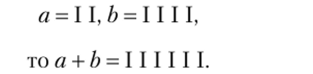
Таким же способом первоклассники порождают новый объект К + 3, приписывая к кружочкам звездочки.

Из определения сложения следует, что если а < Ь, то, сравнивая Ъ с а, мы можем найти представление Ъ в виде а + с, где с снова является цифрой, следовательно, а < а + с. Этим поясняется смысл неравенств и равенств. Для такой наглядно определенной операции сложения выполняются арифметические законы.

Непосредственно из определения следует закон ассоциативности, согласно которому для произвольных цифр а, b, с имеет место равенство.

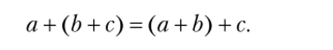
Для доказательства коммутативности необходимо воспользоваться методом полной индукции с позиции такой элементарной точки зрения. Пусть рассматривается некоторое высказывание, относящееся к произвольной цифре. Пусть это высказывание верно для цифры 1 и пусть известно также, что всякий раз, когда оно верно для цифры п, оно верно также и для цифры п + I. Тогда делаем вывод, что оно верно и для любой цифры.

Действительно, любая цифра а строится, начиная с I, путем ряда последовательных присоединений этой цифры. Так как наше высказывание верно для цифры I, и при каждом присоединении этой цифры оно в силу сделанного предположения оказывается верным и для вновь полученной цифры, то в момент завершения построения а придем к выводу, что это высказывание верно для а.

Таким образом, мы имеем дело не с каким-то самостоятельным принципом, а лишь с некоторым следствием, извлекаемым из того факта, что построение цифр производится конкретным образом.

С помощью этого способа умозаключений можно показать, что для любой цифры а

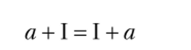
и на основании этого, что всегда справедливо равенство 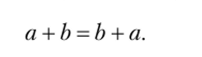Для младших школьников равенство.

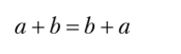
может быть показано наглядно так, как показано на рис. 3.1, соответствующим построением цифр, где а задано последовательностью кружочков, а b — последовательностью квадратиков.

Рис. 3.1. Иллюстрация равенства а + b = b + а.

Из рисунка очевидно, что количество кружочков и квадратиков может быть каким угодно, лишь бы только оно было одинаковым в обеих строках, а значит, сумма не изменяется, если порядок слагаемых изменить.

Умножение цифр определяется следующим образом: произведение а • b означает цифру, которая получается из цифры b замещением в процессе ее порождения каждой цифры I цифрой а так, что мы сначала производим цифру b, а затем при построении цифры а • b всякий раз вместо присоединения I производим присоединение а. Например, если а = I I, b = I I I, то а • b = 11 111 I.

Если ввести сокращенную запись цифр, то, например, произведение 2 • 3 наглядно можно представить так, как на рис. 3.2, где каждый кружочек, представляющий число 3, замещается звездочками, представляющими 2.

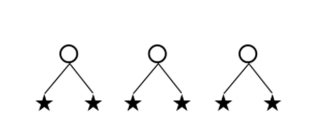
Рис. 32. Иллюстрация произведения 2 • 3.

Заметим, что такое определение умножения согласуется с определением, принадлежащим Н. И. Лобачевскому: произведение а на b производится из а так же, как b производится из единицы. Другими словами, чтобы найти произведение а на Ь, надо каждую единицу числа b «заместить» числом а.

Из этого определения умножения непосредственно с помощью метода полной индукции могут быть получены закон ассоциативности, закон дистрибутивности умножения относительно сложения справа и слева, закон коммутативности умножения. Так как метод полной индукции младшим школьникам недоступен, то указанные свойства умножения при традиционных подходах раскрываются методом неполной индукции. Изучаемые свойства могут быть представлены для частных случаев наглядно. Например, на рис. 3.3 показано равенство 2 3 = 3−2, где сначала каждый из трех кружочков заменяется двумя квадратиками, а затем каждый из двух кружочков заменяется тремя квадратиками. Убеждаемся, что количество произведенных квадратиков одинаково.

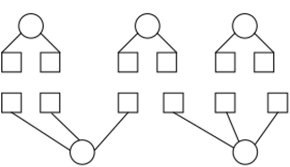
Рис. 3.3. Иллюстрация равенства 2 • 3 = 3 • 2.

Чтобы определить деление, заметим, что построение какой-либо цифры осуществляется путем построения конкретного ряда цифр, который начинается с цифры I и оканчивается цифрой а. Следовательно, кроме самого а этот ряд содержит лишь цифры, меньшие а, и все цифры, меньшие а, встречаются в этом ряду. Назовем эту последовательность рядом цифр от I до а.

Пусть b — отличная от I цифра, такая, что b < а. Тогда b имеет вид I + с и поэтому

значит, а < b а. Умножим b последовательно на цифры из ряда от I до а. Тогда в полученном ряде цифр

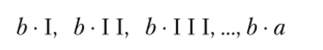
первая цифра меньше а, а последняя больше а. Если идти по этому ряду, то встретим цифру, которая больше а, а предыдущая либо равна а> либо меньше а. Пусть это будет b • q и выполняется.

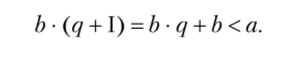
Тем самым либо а представляется в виде а = b • q, либо а = b • q + г и г < Ь. В первом случае а делится на b, во втором случае имеет место деление с остатком. Вообще, а делится на b, если среди цифр ряда.

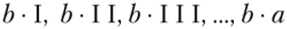
встречается цифра Ь • q.

Из определения делимости вытекает, что если а делится на b, то установление факта делимости дает представление в виде a = b q. Верно и обратное: из равенства a — h-q следует, что а делится на /?, так как цифра q содержится среди цифр от I до а. Другими словами, чтобы разделить а на Ь> надо построить произведения b на цифры I, I I, …, пока не дойдешь до цифры, равной а, или такой, что произведение меньше а, но следующее за ним больше а.

Такой способ содержательных рассуждений над наглядно конструируемыми объектами в виде мысленных экспериментов придерживается принципов: 1) материальной представимости объектов; 2) выполнимости операций над этими объектами. Опыт, приобретаемый ребенком в дошкольном детстве, согласуется с данными принципами.

Задания для самостоятельной работы

• 1. Опишите, как организуется овладение младшими школьниками процессом счета предметов при обучении математике в рамках УМК «Школа России».
• 2. Опишите связи процессов счета и формирования первых представлений о сложении и вычитании чисел в теме «Числа 1 — 10. Число 0» при обучении математике в рамках УМК «Перспектива».
• 3. Опишите методику ознакомления детей с новым числом по УМК «Школа России». Раскройте связи этой методики с гильбертовской концепцией числа как особого рода наглядно представимого объекта, называемого цифрой.
• 4. Определите, с помощью каких упражнений раскрывается порядок следования чисел по УМК «Перспектива». Опишите практические действия детей, необходимые для организации деятельности детей для успешного выполнения данных упражнений. Раскройте организацию деятельности детей при переводе практических действий на язык знаков-индексов. Какие графические знаки при этом можно было бы использовать?
• 5. На смарт-доске даны 2 яблока и 3 груши и запись: 3? 2. Какое задание вы сформулируете к этой ситуации? Чем, по вашему мнению, следует дополнить данную иллюстрацию, чтобы выполнение этого задания детьми способствовало формированию представлений о сложении чисел?
• 6. На смарт-доске выставлены цифры и квадраты:

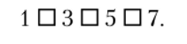
Сформулируйте задание к этой ситуации. Опишите цель вашего задания и организацию деятельности детей по его выполнению.

• 7. Опишите организацию деятельности детей в форме программы действий при выполнении следующего задания: «Каждый знак последовательности Ий И ЕЗ замени парой знаков ® (c)». В каком виде вы представите программу действий для детей? Какие средства вы предоставите детям, чтобы каждый мог выполнить это задание сам, своими руками? Укажите цель выполнения данного задания.
• 8. Опишите организацию деятельности детей при выполнении следующего задания: «Заметь закономерность и продолжи ряд так далеко, чтобы последние соседние произведения в полученном ряду заключались между 22 и 30: 4 х 2, 4 х 3, 4 х 4,…». Укажите познавательную цель данного задания.