Теорема существования и единственности решения

Уравнение.

или, (*).

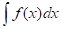
Где — неизвестная функция от, а — заданная функция, является простейшим дифференциальным уравнением. Для его решения, т. е. для отыскивания неизвестной функции, нужно проинтегрировать данную функцию. При этом, как известно, мы получим бесчисленное множество функций, каждая из которых будет удовлетворять условию (*). В этой главе нам удобнее будет под интегралом понимать какую-либо одну первообразную. Тогда любое решение уравнения (*) запишите в виде.

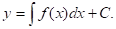
Гораздо чаще приходится иметь дело с уравнениями более сложного вида.

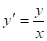
, и Заменяя через, эти уравнения можно переписать в дифференциальной форме:

.

Так как производную можно представить в виде отношения дифференциалов, то уравнение может содержать не производную, а дифференциалы неизвестной функции и независимой переменной.

Дифференциальные уравнения первого порядка в общем виде:

(1).

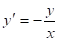
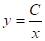
Простевшие примеры показывают, что дифференциальное уравнение может иметь бесчисленное множество решений. Мы наблюдали это уже на примере уравнения (*). Простой проверкой легко убедиться также, что уравнение имеет решениями функции, а уравнение — функции, где — любое число.

Как мы видим, в решения приведенных дифференциальных уравнений входит произвольная постоянная; придавая ей различные значения, мы будем получать разные решения.

Придавая произвольной постоянной определенные числовые значения, мы будем получать частные решения.

Выше мы видели, что уравнение имеет обще решение. Зададим начальное уравнение. Подставив эти значения и в общее решение, получим, откуда. Следовательно, функция удовлетворяет как дифференциальному уравнению, так и начальному условию.

Вопрос о том, в каком случае можно утверждать, что частное решение дифференциального уравнения, удовлетворяющее данному начальному условию, существует, а также что оно будет единственным, выясняется теоремой.

Теорема существования и единственности решения. Если функция непрерывна в области, содержащей точку, то уравнение имеет решение такое, что .

Если, кроме того, непрерывна и частная производная, то это решение уравнения единственно.

Интересно отметить, что в условии теоремы не требуется существования производной .

Теорема эта впервые была сформировано и доказана Коши. Поэтому часто задачу отыскания частного решения по начальным условиям называют задачей Коши.