Некоторые известные несобственные интегралы

Перечислим некоторые известные несобственные интегралы.

1. Интегральные синус и косинус.

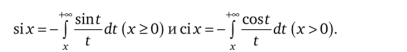
2. Интеграл Эйлера — Пуассона.

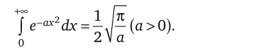
3. Интегралы Френеля.

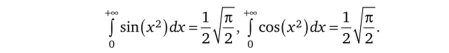
4. Интегралы Эйлера.

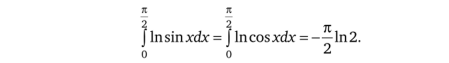
5. Интеграл Дирихле.

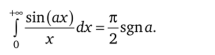
6. Интегралы Лапласа.

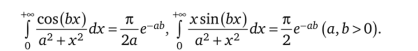
7. Гаммаи бета-функции.

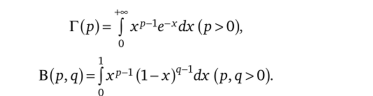
8. Интегралы Фруллани.

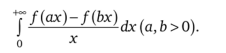
Контрольные задания и задачи для самостоятельного решения

Задачи на свойства и вычисление несобственных интегралов ь.

4.1. Можно ли сходящийся несобственный интеграл 2-го рода J/ (x)dx.

а

от неограниченной функции/, определенной на отрезке [а, Ь], рассматривать, по аналогии с собственным интегралом, как предел соответствую;

п-1.

щей интегральной суммы X /) А*к> ^гд^{е х}к-^>к- *fc+l ^и = ^хк+1 ~^хк?

к=О.

+оо.

4.2. Пусть интеграл J f (x)dx (1) сходится и функция ср ограничена.

а

+(c)о Обязательно ли сходится интеграл J /(x)cp (x)dx (2)? Привести соот;

а ветствующий пример. Что можно сказать о сходимости интеграла (2), если интеграл (1) сходится абсолютно?

• 4.3. Пусть функции/и g определены на конечном (или бесконечном) промежутке [а, Ь] и имеют на нем (или на каждой его конечной части — если промежуток бесконечен) конечное число особых точек. Доказать, что:
  • а) если интегрируема функция /², то и сама функция / будет абсолютно интегрируема (про такую функцию принято говорить, что она «интегрируема с квадратом»);
  • б) если обе функции интегрируемы с квадратом, то и их сумма f + g также интегрируема с квадратом;
  • в) при тех же предположениях и произведение / • g будет абсолютно интегрируемой функцией.
• 4.4. Найти среднее значение на интервале (0, + следующих функций:

a) /(x) = sin²x + cos²(x/2); б) f (x) = fxsinx.

4.5. Пусть /еС[0, + °°) и /(*)—"А при х—Найти lim jf (nx)dx.

п-н~о.

4.6. Вычислить интегралы:

К К

2 2

a) Jln (sinx)dx; б) Jln (cosx)dx;

о о я/.

/2 Wv*.

в) j ~Y- ₂-т~₂-Г~ (^аЬ * о).

о a² sm² х + о² cos² х.

4.7. Найти главные значения интегралов:

⁺°° 1 + х +" +~.

a) f—dx; б) [ arctgxdx; в) [ cosxdx.

— о" 1 + х²

Исследование несобственных интегралов на сходимость

4.8. Убедившись, что интеграл несобственный, не вычисляя его, исследовать его на сходимость:

^З_г x²dx ^ x²dx ⁺~ _ч __VJ

а)—--г; б) J.; в) J х⁵е ^Xdx.

i (^-l)⁵ i л/(х-1)² о.

4.9. Убедившись, что интеграл несобственный, исследовать его на сходимость:

ч ⁺Г1 + х² ^ jc^arctg^r } dx.

• а)(~^Л;бЧл^‘^Ь;в,1^п^Л;
• ^{Г))———; д) +f fl-cos—)dx. otgx-x j V x)}
• 4.10. Используя первый и третий признаки сравнения, исследовать на сходимость несобственные интегралы:
  • а) 7 ^{i—: б) 7 -У 7-А; В) {у2* dr;}

^{I х‘-г2+1, T dx W Лг}

^r) J з/ ₂ ^{; д)} J / ,;

X-Vx2+1 oVx + VxW^.

4.11. Используя третий признак сравнения, исследовать сходимость следующих интегралов (в зависимости от значений параметра):

К

Л г dx ^.

а) I—ах;

о sinPxcos^x.

+°° р б) J ^{m V y}dx, где Р_ш (х) и Р" (х) — взаимно простые (не имеющие о Рп ^х)

общих корней) многочлены соответственно степеней тип;

+°° у-т.

• в) f ——dx (п>0).
• 4.12. Используя разложение подынтегральной функции по формуле Тейлора в окрестностях особых точек, исследовать (в зависимости от значений параметров) сходимость следующих интегралов:
  • а) 7(а*0); б) 7
• 0 X'¹ 1 хР

х²

} «(1 1 7,. }cosx-e 2.

• в) J
• 4.13. Используя признаки Дирихле или Абеля, исследовать сходимость следующих интегралов:

a) J cos (^a^)dx (n>0); б) J ^^-dx (a>, p>0);

0 ^{1 +} *" a ^xP

+oo +" J / 1.

• в) J cos (x²)dx; r) J — arccos — dx. о i^x x² J
• 4.14. Используя критерий Коши расходимости несобственных

⁺Гsinx, ⁺Гcosx ,.

интегралов, доказать расходимость интеграловах и —ах

а ^ХР а ^ХР

• (а>0,р<0).
• 4.15. Исследовать сходимость интегралов (б — в зависимости от значений параметра р):

. ⁺Гsinx, «⁺Гsinx ,.

а) —ах; б) —ах.

о^х о ^х

• 4.16. Используя в том числе второй признак сравнения, исследовать сходимость интегралов (а, б — в зависимости от значений параметров):
  • а) в)

хР1пЧх ³₀ Х^п q ¹ — X²

• 4.17. Исследовать (в зависимости от значений параметра) сходимость следующих интегралов:
• 1 уП +оо 4оо orpfry V*
• а) } dx; б) Г (р)= J xP~¹e~^xdx; в) J-— dx (п>0);

ovl-x⁴ о о 2 + х'¹

iMcosxf¹* .⁺Г _1|Р,.

г) J—²—-dx; д) j x"|x-l|^pdx.

о ^хР о.

+оо.

4.18. Пусть интеграл J f (x)dx сходится и равен J. Доказать, что интеграл J /^х-—jdx также сходится и равен J.

Исследовать сходимость следующих интегралов.

4.19. J-—-. 4.20. Г-—-.

о l + x⁴sin²x о l + x²sin²x.

4.21. 4.22.

ое*-cosx о х + 1.

4.23. jln (sinx)dx. 4.24. J ^ln(^sinx) dx.

о о х

4.25. J-(neN). 4.26. J х^хе~^х" dx (п е К).

о 1 + (1пх)" о.

4.27. J х" е х²)dx (п е R). 4.28. J sin²^7i^x+—jjdx.

Исследование несобственных интегралов на абсолютную (условную) сходимость.

4.29. Исследовать на абсолютную и условную сходимость интегралы: a) J ^С°^^Хdx; б) J x²cos(e^x)dx;

^Jo 1 + ХЧ {.

• 0 1 + X2
• 4.30. Исследовать на абсолютную и условную сходимость интегралы: _а) }SS!m_dx. ₆₎}c°s (V (l-*))

⁺Гsinxarctg¹? x, ,. ⁺T^sin(^{J<: + Jir2}) A

B) J-f—dx (p, q>0); r) J—^y—-'-dx.

• 0 ^X
• 4.31. Исследовать на абсолютную и условную сходимость интегралы:

Я.

a) f, =-; б) f '^^xcosx dx; в) Jsin (secx)dx; г) f ^^m ^sinxdx,

0у]х (е^х -е~^х) J + Ю0 ^J₀ ^J" P"(*).

где P_m (x) и P" (x) — целые многочлены и P_n (x) > 0, если x > a > 0.

.