Степенной метод. 
Численные методы. 
Основы научных вычислений

Степенной метод используется в основном для вычисления доминирующего собственного значения и соответствующего ему собственного вектора. Он не является универсальным методом, но может быть полезен в ряде ситуаций, например в случае больших разреженных матриц. В дополнение схема этого метода демонстрирует некоторые важные аспекты вычисления собственных значений.

Степенной метод является итерационным процессом для нахождения собственных векторов матрицы А. Вначале проведем некоторый предварительный анализ. Возьмем произвольный начальный вектор х⁽⁽⁾⁾. Предположим, что все собственные значения различны по абсолютной величине. Разложим вектор х⁽⁽⁾⁾ по собственным векторам матрицы А:

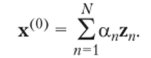
Умножая вектор х⁽⁰⁾ k раз на матрицу А, получим.

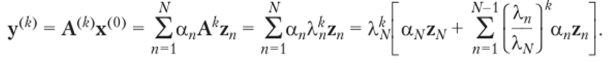
Когда k —³? оо, у^ стремится к вектору, коллинеарному с вектором гдг. Поэтому последовательные степени матрицы, А дают информацию о ее собственном значении X_N. Величина этого собственного значения может быть легко найдена: учитывая второе свойство отношения Рэлея, р (у^) стремится к Хдг, когда k —? оо.

Основываясь на проведенном анализе, можно предложить следующую реализацию степенного метода:

• 1) задать начальный вектор х⁽⁰^;
• 2) для каждого значения k = 0,1,… вычислить у⁽*⁺¹⁾ = Ax^(k);
• 3) следующее приближение вычисляется как =

⁼ У⁽^¹)/||у^(Ь1)|| (эта процедура называется нормализацией, и она предназначена для того, чтобы предотвратить переполнение или исчезновение порядка);

4) если при некотором значении k ||х^⁺¹^ - х^|| < г_р, тогда х^(А+1) есть приближенный собственный вектор z_jV и % = - р (х<*⁺¹>) есть приближенное максимальное по модулю собственное значение Х^.

Сходимость степенного метода. Если все Х_п различны и (zjv, х^<0)) * О, тогда.

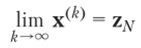
и справедлива следующая оценка.

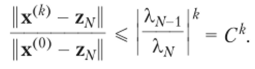
Таким образом, скорость сходимости степенного метода зависит от того, насколько X_N_ _t| меньше, чем X_N.

Пример 4.2 (степенной метод) Рассмотрим следующую матрицу:

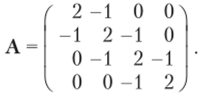
Выберем начальный вектор х⁽⁰⁾ = (1, О, О, О)¹ и г_р = 10~⁵. Результаты вычислений приведены в табл. 4.1.

Таблица 4.1

Видно, что приближения х^(к) довольно медленно сходятся к zдг, так как эта матрица имеет собственные значения

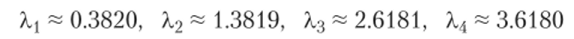
и, следовательно, асимптотическая константа сходимости С =.

⁼ А. дг _ i/X-дг ~ 0.7236.

Если нам нужно вычислить только собственное значение симметричной матрицы А, то можно выполнить гораздо меньшее число итераций. Пусть x^(/l) есть некоторое приближение к z_n, такое, что ъ_п = х^ и ||е^|| = 5. Отношение

Рэлея для вектора х^ имеет вид

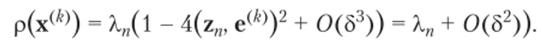
Это выражение показывает, что р (х⁽^) сходится квадратично к Х_ПУ в то время как приближения х^(А) в степенном методе сходятся линейно к z_n. Например, как видно из примера 4.2, нужно только 18 итераций для того, чтобы вычислить А, дгС точностью до четырех знаков.