Элементы математической статистики

Выборка и ее характеристики

Исходным материалом для всякого статистического исследования служит совокупность из п наблюдений, в результате которых случайная величина (сл. в.) X принимает значения х_1; х₂, …, х". В дальнейшем будем предполагать, что испытания взаимно независимы и произведены в неизменных условиях, а функция распределения Р (х) сл. в. X неизвестна, хотя считается принадлежащей конкретному классу распределений Р.

Определение. Набор наблюдаемых значений х_х, …, х" называется повторной выборкой объема п из совокупности Q или просто выборкой.

Определение. Любая функция от результатов наблюдения называется статистикой.

Если статистика используется или хотя бы претендует на таковое для оценивания, то о ней говорят как об оценке.

Эмпирическая функция распределения

Рассмотрим выборку Xj, …, х". Перегруппировав ее элементы в возрастающем порядке:

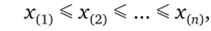
получим упорядоченную выборку, которая называется вариационным или статистическим рядом, а величины х_(|) — порядковыми статистиками.

Обозначим v"(x) — число выборочных значений, не превосходящих х.

*,, v"(x) число тех i, для которых х. < х

Функция F"(x) = - = ;

п п

представляет частоту события {X < х} в последовательности п наблюдений. Ее называют эмпирической функцией распределения выборки.

График функции распределения представлен на рис. 1.1.

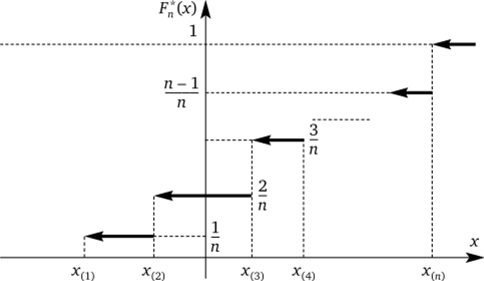
Рис. 1.1. График функции распределения.

Эмпирическая функция распределения обладает всеми свойствами распределения:

• 1) 0 < F*(x) < 1,
• 2) F~ (х) монотонно возрастает.

Она является естественной оценкой теоретической функции распределения F (x), но не совпадает с последней. Если все X; различны, то скачки эмпирической функции распределения равны 1/п и F (x_y)) = j/n. В общем случае скачок функции F" (х) в точке Ху, равен.

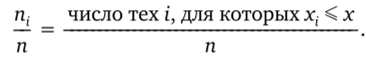
Покажем, чтоЕ*(х) сходится по вероятности к F (x) при п —? оо.

1.1. Выборка и ее характеристики Теорема. Для любого х е R и любого е > 0:

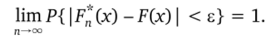
Теорема (Гливенко). Пусть F (x) — функция распределения сл. в. X и F_n'(x) — эмпирическая функция распределения результатов п независимых наблюдений над величиной X, тогда при п —? °о.

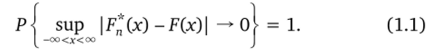
Эта теорема устанавливает важный факт сближения эмпирической функции распределения с теоретической, но не указывает, с какими вероятностями могут возникать те или иные отклонения.

Решение возникающей задачи определения функции распределения величины.

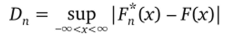
было дано в 1933 г. Колмогоровым.

В приложениях 1—3 приводятся таблицы значений функций распределения, наиболее часто используемых в практических примерах.

Теорема (Колмогорова). Если F (x) — непрерывна, то при.

П —* ОО.

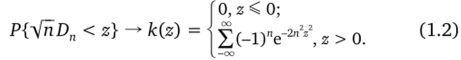
Эта теорема позволяет указать границы, в которых с большой вероятностью будет заключена неизвестная функция распределения F (x). Если z_a подобрано так, что 1 — fc (z_a) = a, то неравенство.

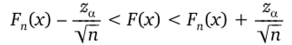
выполняется сразу для всех х с вероятностью, близкой к 1 — а. Действительно,.

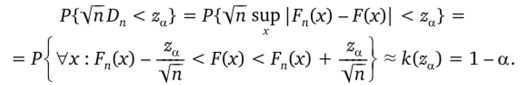
В случае, когда объем выборки очень велик, выборочные значения часто подвергают группировке. Область возможных значений сл. в. разделяют на N непересекающихся интервалов, объединяют выборочные значения, попадающие в каждый из них, и считают, что такие значения по величине равны серединам своих интервалов.

Статистическим аналогом плотности распределения непрерывной сл. в. X может служить гистограмма, которая строится по выборке х_1; х_п следующим образом. Интервал I, содержащий наблюдения, разбивают на N обычно равных интервалов ft:

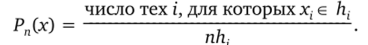
График эмпирической плотности Р*(х) обычно называют гистограммой. Основанием для введения такого аналога служит приближенное равенство Р (х, е h_t) = Jp (x)dx ~.

л,.

~ р (х) • длина ft, справедливое для х, е ft, и малых ft,-.