Существуют ли оптимальные варианты?

Оптимальным называется такой вариант решения, который в рамках ограничений на ресурсы и время решения обеспечивает наилучшее значение некоторого критерия оценки решения.

Понятие оптимальности связано с нахождением экстремума функции, то есть максимума или минимума функции в некотором диапазоне изменения аргумента. При этом существуют определенные особенности нахождения оптимальных вариантов. Поясним это с помощью примера. Допустим, что решение ЛПР определяется функцией Y, зависящей только от одного аргумента х.

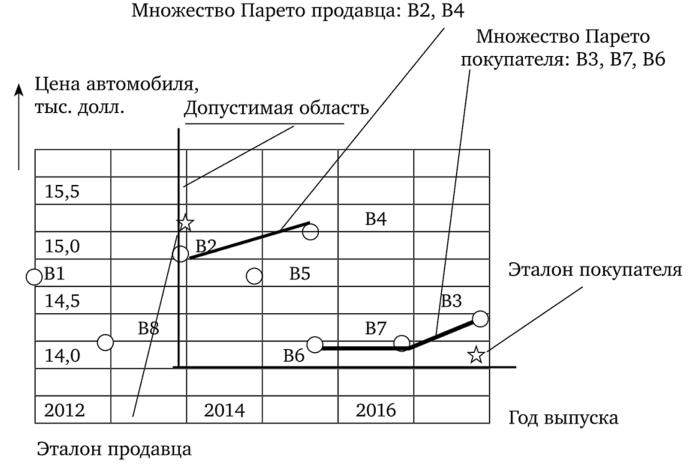
Рис. 7.8. Эталоны (идеалы) и наихудшие варианты покупателя и продавца

Оптимальным вариантом решения для ЛПР является выбор таких значений аргумента х, которые обеспечивают наибольшие или наименьшие значения Y.

В общем случае, функция У (х), которую назовем функцией цели решения, неизвестна, но предположим, что эта зависимость уже известна, она непрерывна, гладкая и имеет следующий вид (рис. 7.9).

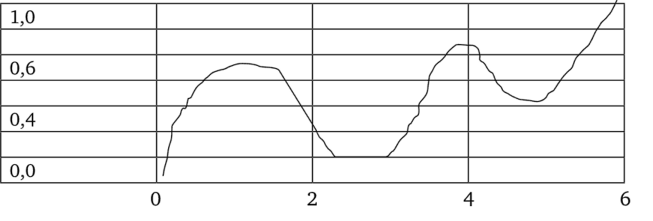
Рис. 7.9. Функция цели решения

Из графика видно, что эта функция принимает экстремальные значения при следующих соотношениях значений аргумента:

Максимальных значений функции два: при аргументе 1 функция равна 0,8 и при аргументе 4 функция равна 0,9.

Минимальных значений тоже два: при аргументе 2,7 функция равна 0,38 и аргументе 5 функция равна 0,56.

Это значит, что один из максимумов больше другого, а один из минимумов меньше другого. В этом случае можно сделать следующие утверждения.

• 1. Если функция неизвестна и поиск решения заключается в нахождении максимума или минимума, то нужно искать все максимумы и все минимумы и среди них выбирать наибольший максимум или наименьший минимум. Эта задача в математике называется поиском глобального экстремума.
• 2. Если мы посмотрим на график еще раз, то увидим, что на граничном справа значении аргумента х нашей функции Y = Дх) величина функции еще больше самого большого из максимумов, хотя это значение функции не является максимумом. Величина функции при левой границе диапазона изменения аргумента меньше самого малого из минимумов, хотя это значение функции тоже не является минимумом. Поэтому надо иметь в виду следующее.

При поиске наибольшего или наименьшего значения некоторой функции следует оценить значения функции на границах изменения аргумента и сравнить их со значениями максимумов и минимумов. В результате сравнения следует выбрать наибольшее или наименьшее значение и соответствующее им значение аргумента.

3. В общем случае функция, определяющая решение, может иметь разрывы в рассматриваемом диапазоне изменения аргумента, то есть состоять из отдельных участков. Например, как на следующем графике (рис. 7.10).

Функция на данном графике имеет разрыв при значениях аргумента от 70 до 95 и не имеет экстремальных значений. Поэтому наибольшие и наименьшие значения функции в этом случае следует выбирать на границах диапазона изменения аргумента. Условием существования максимума или минимума является равенство нулю первой производной функции. При этом функция может быть непрерывна в заданном диапазоне изменения аргумента, внутри которого может не быть ни максимума, ни минимума в этом смысле. Например, как на графике функция при аргументе, равном 6, имеет острый пик, в котором невозможно вычислить производную, она просто не существует. Если решение состоит в том, чтобы найти наибольшее значение в данном диапазоне аргумента, то при аргументе, равном 6, функция достигает наибольшего значения (рис. 7.11).

4. Если функция, определяющая решение, аналитическая, то есть представлена некоторым математическим выражением, то такая функция теоретически может принимать даже бесконечное значение. Поэтому, для практических целей такая функция может быть ограничена приемлемым для реальных условий решения значением.

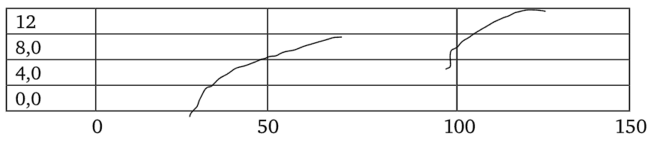
Рис. 7.10. Функция цели с разрывами

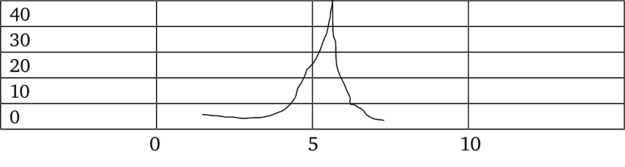
Рис. 7.7 7. Функция цели с пиком.

5. Завершая введение в правила принятия оптимальных решений, отметим важный принцип определения оптимальных вариантов, который называется принципом «субоптимальности».

Принцип су б оптимальности связан с представлением объекта управления как системы и состоит в том, что оптимизация какой-либо подсистемы объекта управления не гарантирует оптимальности всего объекта управления.

Принцип субоптимальности нарушается довольно часто. ЛПР, ответственному за какую-либо подсистему, всегда хочется обеспечить лучшие условия для функционирования своей подсистемы. При этом нарушается пропорциональность развития каждой подсистемы и комплексность подхода к развитию всей системы.

Например, для существования и развития государства как системы необходимо поддерживать и пропорционально развивать такие подсистемы как: сохранность границ, оборона, экономика, промышленность, сельское хозяйство, торговля, финансы, банки, социальное обеспечение и пр. При естественных ограничениях на ресурсы для развития системы, которые для государства выражаются в виде бюджета, повышенная поддержка какой-то подсистемы, например обороны или социального обеспечения населения, наносит ущерб другим подсистемам государства. Чрезмерная поддержка и оптимизация отдельной подсистемы не гарантирует в комплексе оптимальных условий существования и развития в целом сбалансированной системы.

При оптимизации какой-либо подсистемы говорят о локальной оптимизации, а при оптимизации всей системы говорят о комплексной оптимизации объекта управления. Отметим, что комплексная оптимизация объекта управления является дорогостоящим процессом и зачастую целесообразно применять шаговую, поэтапную реализацию комплексного решения.