Уравнение Пуассона (теорема Гаусса в дифференциальной форме)

Рассмотренная ранее теорема Гаусса связывает заряд q, заключенный в объеме V, и поток вектора D через замкнутую поверхность S, охватывающую этот объем: Ф₀ = q. Устремим объем V и поверхность S к нулю. При этом и заряд, заключенный в этом объеме, и поток, пронизывающий эту поверхность, будут стремиться к нулю.

Однако dq/dV будет совершенно определенной величиной — это объемная плотность заряда р. Из теоремы Гаусса получим:

Справа стоит плотность потока вектора D. Эта величина носит название дивергенции (расходимости):

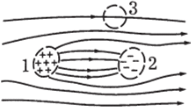
Рис. 4.11.

Соотношение (4.24) и есть уравнение Пуассона или теорема Гаусса в дифференциальной форме. Существенно, что теперь и D и р относятся к некоторой точке, а не к объему или поверхности.

Дивергенция отлична от нуля там, где есть объемный заряд (рис. 4.11, точки 1 и 2). Причем в точке 1 divD положительна, а в точке 2 — отрицательна. В точке 3 diuD = 0.

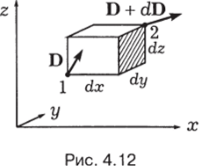
Найдем выражение для дивергенции в координатной форме. Пусть в точке 1 (рис. 4.12) поле характеризуется вектором D, а в точке 2 — вектором D + dD. Вектор D имеет составляющие D_x, D_y, D-, a dD — составляющие dD_It dD_y, dD., причем:

Поток через левую поверхность будет (— dD_xdydz) (со знаком «минус», так как поток входит в замкнутую поверхность, а не выходит). Поток через правую поверхность будет (D_z + + dD_x) dy dz, так что в целом по оси х поток будет dD_:r dy dz. Весь поток через все поверхности будет.

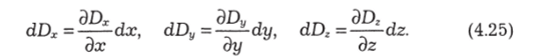
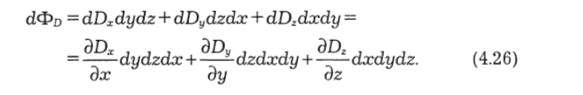
Разделив на dV = dxdydz, получаем для дивергенции выражение.

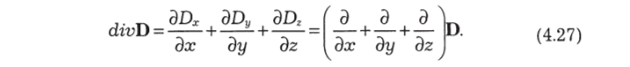
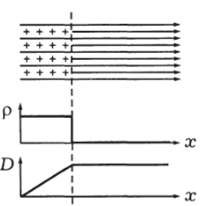
Рис. 4.13.

Дивергенция — это оператор (перечень операций, которые надо проделать с вектором D). Причем это оператор, преобразующий вектор в скаляр (в данном случае — в плотность заряда р).

В одномерном случае, когда чтолибо меняется только по одной координате х, производные по у и по Z равны нулю и dtuD = dD/dx = р. На рисунке 4.13 показано, как в этом случае распределение заряда связано с D.